Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийМатематика (курс 14)Вопрос id:773978 Для вероятности р по выборке объема n с помощью величены 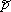 и таблиц нормального распределения строится доверительный интервал. Если увеличить объем выборки в 100 раз, длина доверительного интервала примерно и таблиц нормального распределения строится доверительный интервал. Если увеличить объем выборки в 100 раз, длина доверительного интервала примерно?) увеличится в 100 раз ?) уменьшится в 10 раз ?) уменьшится в 100 раз ?) увеличится в 10 раз Вопрос id:773979 Для контроля качества продукции завода из каждой партии готовых изделий выбирают для проверки 1000 деталей. Проверку не выдерживают в среднем 80 изделий. Равной чему можно принять вероятность того, что наугад взятое изделие этого завода окажется качественным? Сколько примерно бракованных изделий (назовем это число M) будет в партии из 10000 единиц? ?) p = 0.7 ?) p = 0.92 ?) p = 0.8 ?) p = 0.08 Вопрос id:773980 Для построения доверительного интервала для оценки вероятности надо пользоваться таблицами ?) распределения Стьюдента ?) распределения Пирсона ( 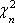 ) )?) нормального распределения ?) распределения Стьюдента или распределения Пирсона ( 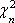 ) )Вопрос id:773981 Для проверки на всхожесть было посеяно 2000 семян, из которых 1700 проросло. Равной чему можно принять вероятность p прорастания отдельного семени в этой партии? Сколько семян в среднем (назовем это число M) взойдет из каждой тысячи посеянных? ?) q=3/20; M=800 ?) p=0.15; M=150 ?) p=17/20; M=750 ?) p=0.85; M=850 Вопрос id:773982 Если вероятность р некоторого события неизвестна, а для оценки этой вероятности производится n испытаний, то 95%-ый доверительный интервал для величины р находится по формуле ?) 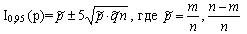 ?) 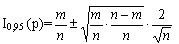 ?) 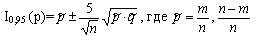 ?) 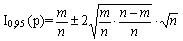 Вопрос id:773985 Если вероятность события A есть р(A), то чему равна вероятность события, ему противоположного? ?) 0.5 ?) 1-р(A) ?) 1 ?) 0 Вопрос id:773986 Если имеется группа из n несовместных событий Hi, в сумме составляющих все пространство, и известны вероятности P(Hi), а событие A может наступить после реализации одного из Hi и известны вероятности P(A/Hi), то P(A) вычисляется по формуле ?) Полной вероятности ?) Муавра-Лапласа ?) Бернулли ?) Байеса Вопрос id:773987 Завод в среднем дает 27% продукции высшего сорта и 70% – первого сорта. Найдите вероятность того, что наудачу взятое изделие не будет высшего или первого сорта. ?) 0.03 ?) 0.27 ?) 0.7 ?) 0.97 Вопрос id:773988 Завод в среднем дает 28% продукции высшего сорта и 70% – первого сорта. Найдите вероятность того, что наудачу взятое изделие будет или высшего, или первого сорта. ?) 0.02 ?) 0.98 ?) 0.7 ?) 0.97 Вопрос id:773989 Задана таблица распределения случайной величины. Найти р(X < 3). 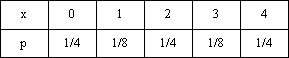 ?) 1/2 ?) 5/8 ?) 3/4 ?) 3/8 Вопрос id:773990 Из колоды, состоящей из 36 карт, вынимают наугад две карты. Вероятность того, что это будут две пики равна ?) 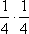 ?) 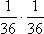 ?) 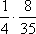 ?) 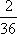 Вопрос id:773992 Изделия изготавливаются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Чему равна вероятность того, что из 200 взятых наугад изделий 2 окажутся неисправными? ?) 0.271 ?) 0.024 ?) 0.001 ?) 0.01 Вопрос id:773993 Изделия изготавливаются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Чему равна вероятность того, что из двух взятых наугад изделий окажутся неисправными оба? ?) 0.01 ?) 0.001 ?) 0.02 ?) 0.0001 Вопрос id:773994 Имеется группа из n несовместных событий Hi, в сумме составляющих все пространство, и известны вероятности P(Hi), а событие A может наступить после реализации одного из Hi, и заданы вероятности P(A/Hi). Известно, событие A произошло. Вероятность, что при этом была реализована Hi вычисляется по формуле ?) Полной вероятности ?) Муавра-Лапласа ?) Байеса ?) Бернулли Вопрос id:773995 Количество поражений шахматиста в течение года имеет распределение Пуассона с параметром λ=6. Вероятность того, что шахматист в течение года проиграет не более двух партий равна ?) 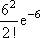 ?) 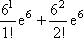 ?) 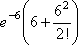 ?) 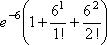 Вопрос id:773997 Количество Х принимаемых по телефону за час звонков имеет распределение Пуассона. Среднее количество принимаемых за час звонков λ=5. Вероятность того, что за час будет принято точно 3 звонка равна ?) 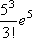 ?) 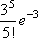 ?) 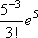 ?) 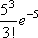 Вопрос id:773998 Куплено 500 лотерейных билетов. На 40 из них упал выигрыш по 1 руб., на 10 – по 5 руб., на 5 – по 10 руб. Найдите средний выигрыш, приходящийся на один билет. ?) 0.28 ?) 2 ?) 1 ?) 0.35 Вопрос id:773999 Лампочки изготавливаются независимо друг от друга. В среднем одна лампочка из тысячи оказывается бракованной. Чему равна вероятность того, что из двух взятых наугад лампочек окажутся исправными обе? ?) 0.998001 ?) 0.98 ?) 0.9 ?) 0.9999 Вопрос id:774000 Монету бросали 100 раз. 70 раз выпал орел, для проверки гипотезы о симметричности монеты строим доверительный интервал и проверяем, попали ли мы в него. По какой формуле строится доверительный интервал, и что даст проверка в нашем конкретном случае? ?) 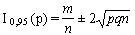 , монета не симметричная , монета не симметричная?) 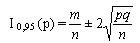 , монета не симметричная , монета не симметричная?) 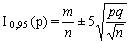 , монета симметричная , монета симметричная?) 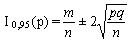 , монета симметричная , монета симметричнаяВопрос id:774002 На некоторой фабрике машина А производит 40% продукции, а машина B – 60%. В среднем 9 из 1000 единиц продукции, произведенных машиной А, и 1 из 250, произведенных машиной B, оказываются бракованными. Какова вероятность, что случайно выбранная единица продукции окажется бракованной? ?) 0.008 ?) 0.006 ?) 0.5 ?) 0.007 Вопрос id:774003 На некотором заводе было замечено, что при определенных условиях в среднем 1.6% изготовленных изделий оказываются неудовлетворяющими стандарту и идут в брак. Равной чему можно принять вероятность того, что наугад взятое изделие этого завода окажется качественным? Сколько примерно непригодных изделий (назовем это число M) будет в партии из 1000 изделий? ?) p = 0.016 ?) p = 0.984 ?) р = 1.6 ?) p = 0.16 Вопрос id:774004 На отрезке длиной 20 см помещен меньший отрезок L длиной 10 см. Найти вероятность того, что точка, наудачу поставленная на большой отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения. ?) 0.1 ?) 0.5 ?) 0.2 ?) 1/4 Вопрос id:774005 При изготовлении детали заготовка должна пройти четыре операции. Полагая появление брака на отдельных операциях событиями независимыми, найти (с точностью до 4-х знаков после запятой) вероятность изготовления нестандартной детали, если вероятность брака на первой стадии операции равна 0.02, на второй – 0.01, на третьей – 0.02, на четвертой – 0.03. ?) 0.0800 ?) 0.9222 ?) 0.0777 ?) 0.9200 Вопрос id:774006 Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора – 0.03, второго – 0.06. Найти вероятность того, что при включении прибора откажет только второй элемент. ?) 0.0671 ?) 0.0582 ?) 0.0938 ?) 0.06 Вопрос id:774007 Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора – 0.05, второго – 0.08. Найти вероятность того, что при включении прибора оба элемента будут работать. ?) 0.928 ?) 0.874 ?) 0.871 ?) 0.826 Вопрос id:774008 Проверяется гипотеза о том, что вероятность выиграть в рулетку 1/37. Доверительный интервал с уровнем доверия 95% строится по формуле 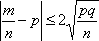 , где , где 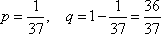 , n – число испытаний, m – количество выигрышей. Сколько надо сделать число ставок (т.е. каким взять n), чтобы отношение числа выигрышей (m к числу n), отличалось от 1/37 не более, чем на 0,01? , n – число испытаний, m – количество выигрышей. Сколько надо сделать число ставок (т.е. каким взять n), чтобы отношение числа выигрышей (m к числу n), отличалось от 1/37 не более, чем на 0,01??) n =500 ?) n =100 ?) n =10 ?) n =900 Вопрос id:774009 Производится n независимых испытаний, в которых вероятность наступления события A равна p. n велико. Вероятность того, что событие A наступит m раз, вычисляется по формуле или используются асимптотические приближения? ?) вычисляется по формуле p(1-p) ?) вычисляется по формуле Бернулли ?) используются асимптотические приближения ?) по формуле Байеса Вопрос id:774010 Производится n независимых испытаний, в которых вероятность наступления события A равна p. Вероятность того, что событие A наступит m раз ?) вычисляется по формуле Байеса ?) равна p(1-p) ?) вычисляется по формуле Муавра-Лапласа ?) вычисляется по формуле Бернулли Вопрос id:774011 Рабочий обслуживает три станка. Вероятность того, что в течение часа станок потребует внимания рабочего, равна для первого станка 0.1, для второго – 0.2 и для третьего – 0.15. Найти вероятность того, что в течение некоторого часа хотя бы один из станков потребует внимания рабочего. ?) 0.612 ?) 0.635 ?) 0.388 ?) 0.365 Вопрос id:774012 Рулетка размечается с помощью меток – 00, 0, 1, ...36. Метки при игре не имеют преимуществ друг перед другом. Игрок делает 114 попыток. Какова вероятность ни разу не выиграть? ?) 0.07 ?) 0.08 ?) 0.05 ?) 0.03 Вопрос id:774013 С первого станка на сборку поступает 40% деталей, остальные 60% со второго. Вероятность изготовления бракованной детали для первого и второго станка соответственно равна 0.01 и 0.04. Найдите вероятность того, что наудачу поступившая на сборку деталь окажется бракованной. ?) 0.028 ?) 0.032 ?) 0.022 ?) 0.024 Вопрос id:774014 Случайная величина X принимает значения 7, -2, 1, -5, 3 с равными вероятностями. Найдите MX. ?) 0 ?) 0.9 ?) 0.7 ?) 0.8 Вопрос id:774015 События A и B называются несовместными, если: ?) р(AB)=1 ?) р(AB)=р(A)+р(B) ?) р(AB)=р(A)р(B) ?) р(AB)=0 Вопрос id:774016 События называются независимыми, если ?) р(AB)=р(A)/р(B) ?) р(AB)=р(A)+р(B) ?) р(AB)=р(B)/р(A) ?) р(AB)=р(A)р(B) Вопрос id:774017 Станок-автомат производит изделия трех сортов. Первого сорта – 80%, второго – 15%. Чему равна вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта? ?) 0.15 ?) 0.2 ?) 0.8 ?) 0.95 Вопрос id:774018 Страхуется 1600 автомобилей; вероятность того, что автомобиль может попасть в аварию, равна 0.2. Каким асимптотическим приближением можно воспользоваться, чтобы сосчитать вероятность того, что число аварий не превысит 350? ?) надо сосчитать по формуле Бернулли, асимптотические формулы дадут большую ошибку ?) локальной формулой Муавра-Лапласа ?) распределением Пуассона ?) интегральной формулой Муавра-Лапласа Вопрос id:774019 Стрелок попадает в цель в среднем в 8 случаях из 10. Какова вероятность, что, сделав три выстрела, он два раза попадет? ?) 0.392 ?) 0.324 ?) 0.384 ?) 0.314 Вопрос id:774020 Студенту предлагают 6 вопросов и на каждый вопрос 4 ответа, из которых один верный, и просят дать верные ответы. Студент не подготовился и выбирает ответы на- угад. Какова вероятность того, что он правильно ответит ровно на половину вопросов? (С точностью до 3-х знаков после запятой) ?) 0.256 ?) 0.164 ?) 0.112 ?) 0.132 Вопрос id:774021 Теннисист идет на игру. Если ему дорогу перебежит черная кошка, то вероятность победы 0,2; если не перебежит, то – 0,7. Вероятность, что кошка перебежит дорогу – 0,1; что не перебежит – 0,9. Вероятность победы ?) 0,1·0,8+0,9·0,3 ?) 0,1·0,2+0,9·0,7 ?) 0,9·0,2+0,1·0,7 ?) 0,1·0,2·0,9·0,7 Вопрос id:774022 Условной вероятностью события B при условии, что событие A с ненулевой вероятностью произошло, называется ?) р(B/A)=р(AB)/р(B) ?) р(B/A)=р(AB) ?) р(B/A)=р(AB)/р(A) ?) р(B/A)=р(AB)р(A) Вопрос id:774023 Человеку, достигшему 20-летнего возраста, вероятность умереть в течение 20 лет равна 0.02. Какова вероятность того, что из 200 застраховавшихся на 20 лет человек в возрасте 20 лет ни один не умрет? ?) 0.0235 ?) 0.0145 ?) 0.256 ?) 0.0183 Вопрос id:774024 Человеку, достигшему 20-летнего возраста, вероятность умереть на 21-м году жизни равна 0.01. Какова вероятность того, что из 200 застраховавшихся человек в возрасте 20-ти лет один умрет через год? ?) 0.246 ?) 0.297 ?) 0.256 ?) 0.271 Вопрос id:774025 Человеку, достигшему 60-летнего возраста, вероятность умереть на 61-м году жизни равна 0.09. Какова вероятность того, что из трех человек в возрасте 60 лет ни один не будет жив через год? ?) 0.999886 ?) 0.000729 ?) 0.999271 ?) 0.000713 Вопрос id:774026 Человеку, достигшему 60-летнего возраста, вероятность умереть на 61-м году жизни равна 0.09. Какова вероятность того, что из трех человек в возрасте 60 лет хотя бы один умрет через год? (с точностью до 4-х знаков после запятой). ?) 0.8281 ?) 0.2464 ?) 0.7536 ?) 0.9100 Вопрос id:774027 Чему равна вероятность достоверного события? ?) 0.1 ?) 1 ?) 0 ?) Может быть любым числом Вопрос id:774028 Чему равна вероятность невозможного события? ?) 1 ?) 0.5 ?) 0 ?) Может быть любым числом Вопрос id:774029 Число грузовых машин, проезжающих мимо бензоколонки, относится к числу легковых машин, как 3:2. Известно, что в среднем одна из 30 грузовых и одна из 25 легковых машин останавливается для заправки. Найти вероятность того, что проезжающая машина будет заправляться. ?) 0.5 ?) 0.33 ?) 0.036 ?) 0.04 Вопрос id:774030 R – множество всех вещественных чисел, Q – множество всех рациональных чисел. Тогда справедливы отношения ?) 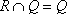 ?) 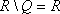 ?) 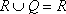 ?) 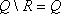 Вопрос id:774033 X – множество студентов группы, Y – множество дисциплин, по которым сдают экзамен. Предикат P (X, Y): “студент Х сдал экзамен по дисциплине Y”. Предикатная формула 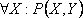 означает: «___» означает: «___»?) все студенты сдали экзамен по предмету Y ?) X сдал экзамен хотя бы по одному предмету ?) X сдал экзамен по всем предметам ?) некоторые студенты сдали экзамен по предмету Y Вопрос id:774034 Верны ли определения? А) Бесконечно убывающей геометрической прогрессией называется геометрическая прогрессия у которой модуль знаменателя меньше единицы В) Бесконечно убывающей геометрической прогрессией называется геометрическая прогрессия у которой модуль знаменателя меньше единицы Подберите правильный ответ ?) А - нет, В - нет ?) А - нет, В - да ?) А - да, В - да ?) А - да, В - нет |
Copyright tests.ithead.ru 2013-2026