Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
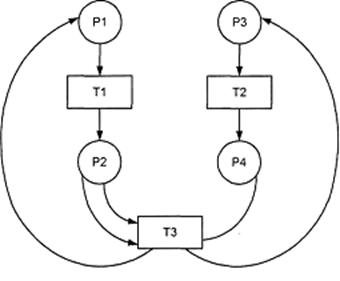
Список вопросов базы знанийТеория систем массового обслуживанияВопрос id:2290675 Тема/шкала: 3307.01.01;МТ.01;1 - Модульный тест - Теория систем массового обслуживания Состояние называется ___, если вероятность попадания в него за конечное число шагов равна нулю ?) случайным ?) возвратным ?) нулевым ?) невозвратным Вопрос id:2290676 Тема/шкала: 3307.01.01;МТ.01;1 - Модульный тест - Теория систем массового обслуживания Состояние называется ___, если среднее время возвращения в него конечно ?) возвратным ненулевым ?) возвратным нулевым ?) эргодическим ?) поглощающим Вопрос id:2290677 Тема/шкала: 3307.01.01;МТ.01;1 - Модульный тест - Теория систем массового обслуживания Состояние называется ___, если среднее время возвращения в него равно бесконечности ?) неприводимым ?) возвратным ненулевым ?) поглощающим ?) возвратным нулевым Вопрос id:2290679 Тема/шкала: 3307.01.01;МТ.01;1 - Модульный тест - Теория систем массового обслуживания Среднее квадратическое отклонение экспоненциально-распределенной случайной величины st (где l - интенсивность) равно ?) 1/l2 ?) 1-l ?) 1/l ?) 1+l Вопрос id:2290680 Тема/шкала: 3307.01.01;МТ.01;1 - Модульный тест - Теория систем массового обслуживания Стационарный ординарный поток без последействия называют ?) мгновенным ?) бесконечным ?) интенсивным ?) простейшим Вопрос id:2290681 Тема/шкала: 3307.01.01;МТ.01;1 - Модульный тест - Теория систем массового обслуживания Стационарный поток с ___ – поток Пальма, задаваемый условной вероятностью φ0(t) отсутствия требований в промежутке длиной t, если в начале этого промежутка было требование ?) опережением ?) ограничением ?) запаздыванием ?) освобождением Вопрос id:2290682 Тема/шкала: 3307.01.01;МТ.01;1 - Модульный тест - Теория систем массового обслуживания Цепь Маркова называется ___, если каждое ее состояние может быть достигнуто из любого другого состояния ?) однородной ?) неприводимой ?) приводимой ?) замкнутой Вопрос id:2290683 Тема/шкала: 3307.01.01;МТ.01;1 - Модульный тест - Теория систем массового обслуживания Чтобы ни одно требование не было потеряно в результате ресурсного конфликта, в системе может быть предусмотрен специальный буфер памяти, в который будут помещаться требования, которые не могут быть обслужены немедленно при поступлении из-за занятости всех серверов. В этом случае говорят, что в системе организуется ?) очередь серверов ?) последовательный трафик ?) очередь ресурсов ?) очередь требований Вопрос id:2290688 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания На рисунке представлена ___ сеть Петри
?) цветовая ?) приоритетная ?) раскрашенная ?) простая Вопрос id:2290729 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания ___ - функция комплексной переменной вида 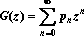 ?) Коммуникационное преобразование ?) Z-преобразование ?) G-преобразование ?) Преобразование равновесия Вопрос id:2290763 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания Для каждого сервера работа 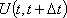 равна ___, если в интервале равна ___, если в интервале 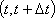 сервер не занят сервер не занят?) Dt ?) 0 или 1 ?) 0 ?) 1 Вопрос id:2290767 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания Для непрерывной однородной цепи Маркова уравнение Чепмена-Колмогорова имеет вид: 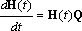 . Здесь матрица H(t) = [ pij(t)] называется матрицей . Здесь матрица H(t) = [ pij(t)] называется матрицей?) дискретного множества значений ?) вероятности перехода из состояния i в состояние j в момент времени t ?) текущего состояния ?) интенсивности переходов Вопрос id:2290768 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания Для непрерывной однородной цепи Маркова уравнение Чепмена-Колмогорова имеет вид: 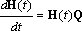 . Здесь матрица Q называется матрицей . Здесь матрица Q называется матрицей?) интенсивности переходов ?) вероятности перехода из состояния i в состояние j в момент времени t ?) текущего состояния ?) дискретного множества значений Вопрос id:2290778 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания Если рассматривать системы массового обслуживания только как серверы, то формула Литтла имеет вид (где 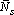 – среднее число заявок в серверах, – среднее число заявок в серверах,  – среднее время обработки в сервере, l - интенсивность) – среднее время обработки в сервере, l - интенсивность)?) 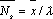 ?) 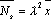 ?) 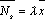 ?) 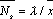 Вопрос id:2290786 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания Интегральное уравнение вида 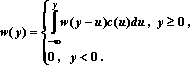 носит название уравнения носит название уравнения?) Лапласа ?) Бернулли ?) Литтла ?) Линдли Вопрос id:2290818 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания Понятие работы характеризует степень занятости (загрузку) серверов только совместно с указанием интервала времени, за который эта работа была выполнена. В большинстве практических случаев используется производная от работы, называемая ___ нагрузкой: 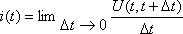 ?) мгновенной ?) средней ?) наибольшей ?) потенциальной Вопрос id:2290820 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания Поток ___ - это ординарный поток, промежутки между требованиями в котором образуют последовательность взаимно-независимых случайных величин: 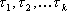 ?) с ограниченным последствием ?) освобождений серверов ?) Пальма ?) без последствий Вопрос id:2290834 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания Случайная величина с плотностью вероятностей, равной 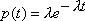 (где l - интенсивность), называется ___ - распределенной (где l - интенсивность), называется ___ - распределенной?) нормально ?) равномерно ?) линейно ?) экспоненциально Вопрос id:2290850 Тема/шкала: 3307.Зач.01;ТБПД.01;1 - Тестовая база по дисциплине - Теория систем массового обслуживания Фундаментальное свойство случайной величины, равной разности между временем обслуживания требования с номером n и промежутком времени между поступлениями n+1 и n-го требования 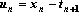 , состоит в том, что для стабильных СМО, т.е. имеющих стационарное распределение вероятностей состояний, ее математическое ожидание должно , состоит в том, что для стабильных СМО, т.е. имеющих стационарное распределение вероятностей состояний, ее математическое ожидание должно?) быть отрицательным ?) равняться нулю ?) быть положительным ?) равняться единице |
Copyright tests.ithead.ru 2013-2026