Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийМатематика (курс 10)Вопрос id:747664 Собственными векторами матрицы системы уравнений 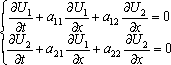 называются собственные векторы матрицы называются собственные векторы матрицы 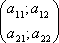 . Тогда собственными векторами матрицы системы уравнений . Тогда собственными векторами матрицы системы уравнений 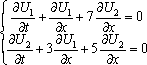 являются векторы являются векторы?) ?) ?) ?) Вопрос id:747665 Собственными значениями матрицы системы уравнений 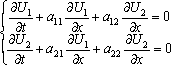 называются корни уравнения второго порядка называются корни уравнения второго порядка 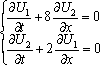 являются значения являются значения?) l1 = -4 ; l2 = 4 ?) l1 = 3 ; l2 = -5 ?) l1 = -1 ; l2 = 1 ?) l1 = -1 ; l2 = 3 Вопрос id:747666 Собственными значениями матрицы системы уравнений 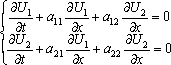 называются корни уравнения второго порядка называются корни уравнения второго порядка 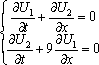 являются значения являются значения?) l1 = -1 ; l2 = 2 ?) l1 = -1 ; l2 = 1 ?) l1 = -3 ; l2 = 3 ?) l1 = -3 ; l2 = 5 Вопрос id:747667 Собственными значениями матрицы системы уравнений 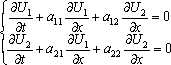 называются корни уравнения второго порядка называются корни уравнения второго порядка 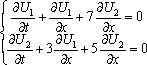 являются значения являются значения?) l1 = -1 ; l2 = 3 ?) l1 = -1 ; l2 = 1 ?) l1 = 3 ; l2 = -5 ?) l1 = -2 ; l2 = 8 Вопрос id:747668 Согласно теореме Лиувилля функция ?) аналитична в плоскости С и ограничена ?) дифференцируема в смысле R2 в плоскости С и ограничена ?) аналитична в плоскости С ?) ограничена в плоскости С Вопрос id:747669 Согласно теореме о полной сумме вычетов имеет место равенство ( ?) ?) ?) ?) Вопрос id:747670 Согласно формуле Эйлера имеет место равенство ?) ?) ?) ?) Вопрос id:747671 Спектр линейного оператора А в евклидовом пространстве R2 A = ?) {-3;10} ?) {-10;3} ?) {- ?) {-0,1; Вопрос id:747672 Сходимость итерационного метода решения систем линейных уравнений зависит от ?) вида матрицы системы ?) начального приближения системы ?) количества нулей в матрице ?) величины правых частей системы Вопрос id:747673 Точка х ⊂ А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества (-1,+∞) является ?) (-1,+ ∞) ?) [-1,+ ∞] ?) (-∞,-1] ?) [-1,+ ∞) Вопрос id:747674 Точка х ⊂ А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества {1;2;3;…} является ?) Ø - пустое множество ?) {1;2;3;…} ?) {0;1;-1;2;-2;…} ?) {0} Вопрос id:747675 Точка х ⊂ А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Множеством предельных точек множества { ?) {0; ?) {0} ?) { ?) Ø - пустое множество Вопрос id:747676 Точка х ⊂ А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества всех рациональных чисел является множество ?) Ø - пустое множество ?) всех рациональных чисел ?) всех иррациональных чисел ?) всех вещественных чисел Вопрос id:747677 Точка х ⊂ А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества решений неравенства х2siny < 1 является множество решений ?) х2siny > 1 ?) х2siny ≥ 1 ?) х2siny = 1 ?) х2siny ≤ 1 Вопрос id:747678 Точка х ⊂ А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества решений неравенства ex + 3x2y4 > 1 является множество решений ?) ex + 3x2y4 < 1 ?) ex + 3x2y4 ≥ 1 ?) ex + 3x2y4 = 1 ?) ex + 3x2y4 ≤ 1 Вопрос id:747679 Уравнение x(t) - ?) Фредгольма первого рода ?) Фредгольма второго рода ?) Вольтерра первого рода ?) Вольтерра второго рода Вопрос id:747680 Уравнение x(t) - ?) Фредгольма второго рода ?) Фредгольма первого рода ?) Вольтерра второго рода ?) Вольтерра первого рода Вопрос id:747681 Уравнение ?) Фредгольма второго рода ?) Вольтерра первого рода ?) Фредгольма первого рода ?) Вольтерра второго рода Вопрос id:747682 Уравнение ?) Фредгольма второго рода ?) Фредгольма первого рода ?) Вольтерра второго рода ?) Вольтерра первого рода Вопрос id:747683 Уравнение ?) Вольтерра первого рода ?) Фредгольма второго рода ?) Фредгольма первого рода ?) Вольтерра второго рода Вопрос id:747684 Уравнение записано в виде, удобном для итераций x=0,5cos2x + π ∕ 8 . Первое приближение метода простой итерации x1 для начального приближения x0=π ∕ 4 равно ?) 3π ∕ 4 ?) π ∕ 4 ?) 3π ∕ 8 ?) π ∕ 8 Вопрос id:747685 Уравнение теплопроводности после преобразования Фурье имеет вид ?) s2u + uxx = 0 ; ?) ut - s2u = 0 ; ?) ut + s2u = 0 ; ?) s2u - uxx = 0 ; Вопрос id:747686 Уравнение х(t) -  ln(t2s - s3)x(s)ds = et является интегральным уравнением ln(t2s - s3)x(s)ds = et является интегральным уравнением?) Вольтерра второго рода ?) Фредгольма второго рода ?) Вольтерра первого рода ?) Фредгольма первого рода Вопрос id:747687 Уравнение х(t) -  cos(t+2s)x(s)ds = cos2t является интегральным уравнением cos(t+2s)x(s)ds = cos2t является интегральным уравнением?) Фредгольма первого рода ?) Фредгольма второго рода ?) Вольтерра второго рода ?) Вольтерра первого рода Вопрос id:747688 Уравнения характеристик для дифференциального уравнения 3ut + 4ux = 0 имеют вид ?) ?) ?) ?) Вопрос id:747689 Уравнения характеристик для дифференциального уравнения 4ut - 3ux = 0 имеют вид ?) ?) ?) ?) Вопрос id:747691 Уравнения характеристик для дифференциального уравнения tut + xux + u = 0 имеют вид ?) ?) ?) ?) Вопрос id:747692 Уравнения характеристик для дифференциального уравнения ut + 4ux = 0 имеют вид ?) ?) ?) ?) Вопрос id:747693 Условие сходимости метода итераций для нелинейного уравнения x = φ( x ) заключается в том, что ?) ?) ?) ?) Вопрос id:747694 Условия Коши-Римана комплексной дифференцируемости функции ?) ?) ?) ?) Вопрос id:747695 Формула метода Ньютона для нелинейного уравнения F( x ) = 0 имеет вид: ?) ?) ?) ?) Вопрос id:747696 Формула метода трапеций для вычисления определенного интеграла имеет вид ?) ?) ?) ?) Вопрос id:747697 Формула метода трапеций для вычисления определенного интеграла по сравнению с формулой метода Симпсона ?) имеет для гладких функций большую точность ?) имеет одинаковую точность ?) имеет для гладких функций меньшую точность ?) имеет для любых функций большую точность Вопрос id:747698 Формула Муавра имеет вид ?) ?) ?) ?) Вопрос id:747699 Фундаментальным решением уравнения Лапласа в пространстве называется функция ?) u0 = ?) u0 = ?) u0 = r ?) u0 = ln Вопрос id:747700 Фундаментальным решением уравнения Лапласа на плоскости называется функция ?) u0 = r ?) u0 = ?) u0 = ln ?) u0 = Вопрос id:747701 Фундаментальным решением уравнения Лапласа на плоскости называется функция ?) u0 = ?) u0 = ?) u0 = ln ?) u0 = Вопрос id:747702 Функция u(x,t) = C(x-at), где С - произвольная функция, является общим решением уравнения ?) ut = a2uxx ?) utt = a2uxx ?) utt + a2uxx = 0 ?) ut + aux = 0 Вопрос id:747703 Функция u(x,t) = C1(x-at) + C2(x+at), где С1 и С2 - произвольные функции, является общим решением уравнения ?) ut = a2uxx ?) utt = a2uxx ?) utt + a2uxx = 0 ?) ut + aux = 0 Вопрос id:747704 Функция u(x,t) = ex+at является решением уравнения ?) utt + a2uxx = 0 ?) ut = a2uxx ?) ut + aux = 0 ?) ut - aux = 0 Вопрос id:747705 Функция u(x,t) = ln(x-at) является решением уравнения ?) utt + a2uxx = 0 ?) ut - aux = 0 ?) ut = a2uxx ?) ut + aux = 0 Вопрос id:747706 Функция u(x,t) = sin(x-at) является решением уравнения ?) ut - aux = 0 ?) utt + a2uxx = 0 ?) ut + aux = 0 ?) ut = a2uxx Вопрос id:747707 Функция u(x,t) = ?) ut + aux = 0 ?) ut - aux = 0 ?) utt + a2uxx = 0 ?) ut = a2uxx Вопрос id:747708 Функция u0(x,y,z) = ?) волнового ?) Пуассона ?) теплопроводности ?) Лапласа Вопрос id:747709 Функция u0(x,y,z) = ln ?) Лапласа ?) Пуассона ?) волнового ?) теплопроводности Вопрос id:747710 Функция ?) плоскость w с выброшенной положительной полуосью ?) внутренность единичного круга ?) плоскость w с выброшенным отрезком ?) верхнюю полуплоскость Вопрос id:747711 Функция ?) верхнюю полуплоскость ?) внешность единичного круга ?) плоскость w с выброшенным отрезком ?) внутренность единичного круга Вопрос id:747712 Функция ?) плоскость w с выброшенным отрезком ?) верхнюю полуплоскость ?) плоскость w ?) плоскость w с выброшенной положительной полуосью Вопрос id:747713 Функция ?) верхнюю полуплоскость ?) плоскость w с выброшенной положительной полуосью ?) плоскость w с выброшенной отрицательной полуосью ?) плоскость w с выброшенным отрезком Вопрос id:747714 Функция Жуковского - это функция вида ?) ?) ?) ?) |
Copyright tests.ithead.ru 2013-2026