Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийМатематика (курс 11)Вопрос id:775519 Алгоритм называется неустойчивым, если ?) малые изменения исходных данных не изменяют окончательный результат ?) большие изменения в исходных данных не изменяют окончательный результат ?) малые изменения исходных данных и погрешности округления приводят к значительному изменению окончательных результатов ?) большие изменения в исходных данных приводят к малому изменению результата Вопрос id:775520 Аппроксимация называется непрерывной, если аппроксимирующая функция φ(x) ?) является непрерывной ?) строится на отрезке [a, b] ?) аппроксимирует исходную непрерывную функцию f(x) ?) является многочленом Вопрос id:775521 Аппроксимация первой производной 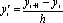 имеет погрешность порядка имеет погрешность порядка?) 1 ?) 0,5 ?) 4 ?) 2 Вопрос id:775522 Аппроксимация первой производной 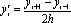 имеет погрешность порядка имеет погрешность порядка?) 2 ?) 3 ?) 1,5 ?) 1 Вопрос id:775523 Аргумент числа z = x + iy (x y > 0) равен ?) 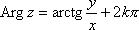 ?) 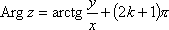 ?) 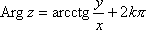 ?) 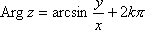 Вопрос id:775524 В окрестности точки z = 0 справедливо разложение ?) 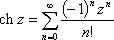 ?) 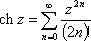 ?) 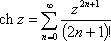 ?) 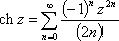 Вопрос id:775525 В таблично заданной функции производная в точке 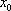 вычислена с использованием шагов h и 2h . Получены величины вычислена с использованием шагов h и 2h . Получены величины 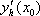 = 0,8 и = 0,8 и 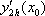 = 0,65. Погрешность формулы для вычисления производных имеет порядок = 0,65. Погрешность формулы для вычисления производных имеет порядок 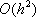 . Тогда уточненное значение производной . Тогда уточненное значение производной 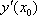 по методу Рунге равно по методу Рунге равно?) 0,87 ?) 0,75 ?) 0,7 ?) 0,805 Вопрос id:775526 В таблично заданной функции производная в точке 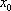 вычислена с использованием шагов h и 2h . Получены величины вычислена с использованием шагов h и 2h . Получены величины 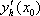 = 1,5 и = 1,5 и 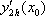 = 1,3. Погрешность формулы для вычисления производных имеет порядок = 1,3. Погрешность формулы для вычисления производных имеет порядок 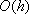 . Тогда уточненное значение производной . Тогда уточненное значение производной 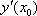 по методу Рунге равно по методу Рунге равно?) 1,7 ?) 1,6 ?) 1,65 ?) 1,4 Вопрос id:775527 В таблично заданной функции производная в точке 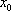 вычислена с использованием шагов h и 2h . Получены величины вычислена с использованием шагов h и 2h . Получены величины 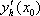 = 2,4 и = 2,4 и 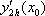 = 2,7. Погрешность формулы для вычисления производных имеет порядок = 2,7. Погрешность формулы для вычисления производных имеет порядок 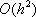 . Тогда уточненное значение производной . Тогда уточненное значение производной 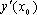 по методу Рунге равно по методу Рунге равно?) 2,457 ?) 2,207 ?) 2,3 ?) 2,5 Вопрос id:775528 Величина 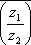 равна равна?) 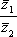 ?) 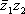 ?) 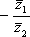 ?) 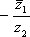 Вопрос id:775529 Верным является утверждение ?) если общий член ряда 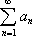 стремится к нулю, то ряд сходится стремится к нулю, то ряд сходится?) ряд расходится, если общий член ряда стремится к нулю ?) ряд сходится, если 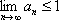 ?) если ряд 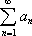 сходится, то его общий член стремится к нулю сходится, то его общий член стремится к нулюВопрос id:775530 Верным является утверждение, что если ?) 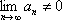 , то ряд расходится , то ряд расходится?) 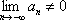 , то ряд расходится , то ряд расходится?) 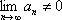 , то ряд сходится , то ряд сходится?) 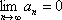 , то ряд расходится , то ряд расходитсяВопрос id:775531 Выбор начального приближения на сходимость или расходимость метода Зейделя при решении систем линейных уравнений ?) не влияет ?) влияет, если матрица не симметричная ?) влияет, если матрица не является верхней треугольной ?) влияет всегда Вопрос id:775532 Вычет функции 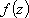 в полюсе а порядка n вычисляется по формуле в полюсе а порядка n вычисляется по формуле?) 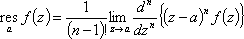 ?) 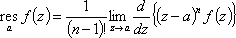 ?) 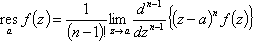 ?) 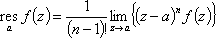 Вопрос id:775533 Вычет функции 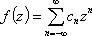 в бесконечности равен в бесконечности равен?) 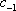 ?) 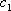 ?) 0 ?) 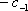 Вопрос id:775534 Вычетом функции 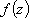 в конечной изолированной особой точке а этой функции называется выражение в конечной изолированной особой точке а этой функции называется выражение?) 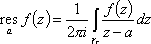 ?) 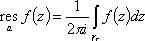 ?) 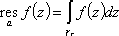 ?) 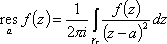 Вопрос id:775535 Гармонический ряд является ?) сходящимся ?) сходящимся абсолютно ?) расходящимся ?) сходящимся условно Вопрос id:775536 Гармоническим рядом называется ряд ?) 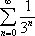 ?) 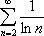 ?) 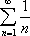 ?) 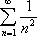 Вопрос id:775537 Гармоническим рядом является ряд ?) 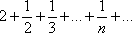 ?) 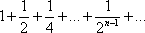 ?) 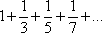 ?) 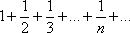 Вопрос id:775538 Гармонической называется функция 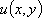 , удовлетворяющая уравнению , удовлетворяющая уравнению?) 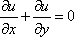 ?) 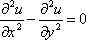 ?) 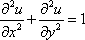 ?) 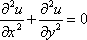 Вопрос id:775539 Дан ряд  ; применив признак Даламбера, получим, что ; применив признак Даламбера, получим, что?) ряд сходится ?) ряд сходится условно ?) требуется дополнительное исследование ?) ряд расходится Вопрос id:775540 Дана система  и задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение и задано начальное приближение (1; 1). Один шаг метода Зейделя дает первое приближение?) (0,6 ; 1) ?) (0,6 ; 1,06) ?) (0,6 ; 1,1) ?) (0,1 ; 1,06) Вопрос id:775541 Дана система уравнений  . Для сходимости итерационного метода ее надо записать в виде . Для сходимости итерационного метода ее надо записать в виде?)  ?) 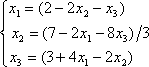 ?) 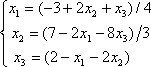 ?) 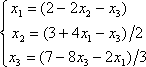 Вопрос id:775542 Дано нелинейное уравнение cos2x - 2x + π ∕ 4 = 0 и начальное условие x0 = π ∕ 4. Первое приближение метода Ньютона x1 будет равно ?) 5π ∕ 16 ?) π ∕ 2 ?) 3π ∕ 16 ?) 3π ∕ 4 Вопрос id:775543 Дано нелинейное уравнение x2 − sinx + 1 = 0 и начальное приближение x0 = 0. Первое приближение x1 в методе Ньютона равно ?) 0,5 ?) 0,1 ?) −1 ?) 1 Вопрос id:775544 Дано уравнение x = sinx + 1 и начальное приближение x0 = π ⁄ 2 . Первое приближение x1 метода простой итераций равно ?) 2 ?) π ?) 0 ?) 1 Вопрос id:775545 Даны два ряда 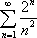 (1) и (1) и 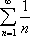 (2); верное утверждение - (2); верное утверждение -?) первый ряд сходится, второй - расходится ?) оба ряда сходятся ?) оба ряда расходятся ?) первый ряд расходится, второй - сходится Вопрос id:775546 Даны ряды 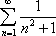 (1) и (1) и 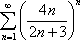 (2); верное утверждение - (2); верное утверждение -?) первый ряд расходится, второй - сходится ?) первый ряд сходится, второй - расходится ?) оба ряда расходятся ?) оба ряда сходятся Вопрос id:775547 Даны ряды 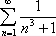 (1) , (1) , (2) и (2) и  (3), верно утверждение, что (3), верно утверждение, что?) три ряда сходятся ?) ряд (1) сходится, ряды (2) и (3) расходятся ?) ряды (1) и (2) сходятся, ряд (3) расходится ?) ряд (1) сходится, ряд (2) расходится, ряд (3) сходится Вопрос id:775548 Даны ряды  (1) и (1) и  (2); верно утверждение - (2); верно утверждение -?) оба ряда сходятся абсолютно ?) оба ряда сходятся условно ?) оба ряда расходятся ?) первый ряд cходится абсолютно, второй - условно Вопрос id:775549 Даны ряды  (1) и (1) и  (2); верное утверждение - (2); верное утверждение -?) первый ряд сходится, второй - расходится ?) оба ряда расходятся ?) оба ряда сходятся ?) первый ряд расходится, второй - сходится Вопрос id:775550 Действительная часть числа z равна ?)  ?)  ?) 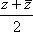 ?) 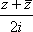 Вопрос id:775551 Для знакоположительного ряда 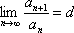 , исследование сходимости ряда с помощью d есть , исследование сходимости ряда с помощью d есть?) предельный признак сравнения ?) признак Даламбера ?) необходимый признак сходимости ?) радикальный признак Коши Вопрос id:775552 Для знакоположительного ряда 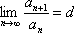 , тогда, если , тогда, если?)  , то ряд сходится , то ряд сходится?)  , то ряд сходится , то ряд сходится?)  , то ряд сходится , то ряд сходится?)  , то ряд расходится , то ряд расходитсяВопрос id:775553 Для знакоположительных рядов 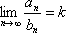 , где , где 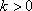 , исследование сходимости ряда с помощью k есть , исследование сходимости ряда с помощью k есть?) радикальный признак Коши ?) признак Даламбера ?) предельный признак сравнения ?) необходимый признак сходимости Вопрос id:775554 Для линейной системы уравнений вычисления по итерационной формуле 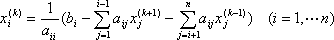 называют методом называют методом?) релаксации ?) Зейделя ?) Ньютона ?) такого метода нет Вопрос id:775555 Для линейной системы уравнений вычисления по итерационной формуле 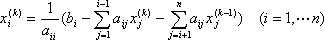 называют методом называют методом?) Ньютона ?) Гаусса ?) Простой итерации ?) Зейделя Вопрос id:775556 Для матрицы A = 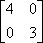 метод Зейделя x(k+1) = Ax(k) будет метод Зейделя x(k+1) = Ax(k) будет?) сходящимся при начальном векторе  ?) сходящимся при начальном векторе  ?) расходящимся ?) сходящимся Вопрос id:775557 Для однолистности отображения 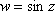 в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек 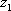 и и 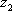 , связанных соотношением , связанных соотношением?) 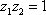 ?) 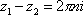 ( (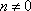 - целое) - целое)?) 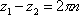 ( (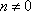 - целое) - целое)?) 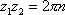 ( (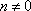 - целое) - целое)Вопрос id:775558 Для однолистности отображения 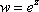 в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек в области D необходимо и достаточно чтобы область D не содержала никаких двух различных точек 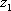 и и 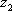 , связанных соотношением , связанных соотношением?) 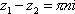 (n - целое) (n - целое)?) 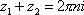 (n - целое) (n - целое)?)  (n - целое) (n - целое)?)  (n - целое) (n - целое)Вопрос id:775559 Для решения нелинейного уравнения второй порядок сходимости имеет метод ?) простой итерации ?) половинного деления ?) Ньютона ?) Гаусса Вопрос id:775560 Для ряда  общий член равен общий член равен?)  ?) 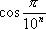 ?) 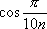 ?) 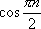 Вопрос id:775561 Для таблично заданной функции 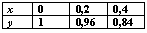 значение y(0,3) , вычисленное с помощью линейной интерполяции равно значение y(0,3) , вычисленное с помощью линейной интерполяции равно?) 0,94 ?) 0,9033 ?) 0,9 ?) 0,88 Вопрос id:775562 Для таблично заданной функции  Результат линейной интерполяции при x=0.1 дает значение Результат линейной интерполяции при x=0.1 дает значение?) 0,97 ?) 1,02 ?) 0,95 ?) 0,98 Вопрос id:775563 Для таблично заданной функции  значение y(0,1) , вычисленное с помощью квадратичной интерполяции равно значение y(0,1) , вычисленное с помощью квадратичной интерполяции равно?) 0,03 ?) 0,028 ?) 0,02 ?) 0,04 Вопрос id:775564 Для того чтобы ряд сходился, необходимо и достаточно, чтобы ?)  ?)  ?) 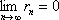 ?) 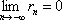 Вопрос id:775565 Для того чтобы функция 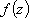 определенная в окрестности точки определенная в окрестности точки 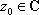 имела в этой точке производную необходимо и достаточно чтобы имела в этой точке производную необходимо и достаточно чтобы?) 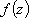 была дифференцируема в точке была дифференцируема в точке 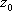 в смысле R2 в смысле R2?) 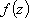 имела конечный предел в точке имела конечный предел в точке 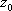 ?) 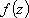 была дифференцируема в точке была дифференцируема в точке 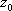 в смысле С в смысле С?) 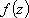 была непрерывна в точке была непрерывна в точке 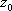 Вопрос id:775566 Для функции 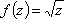 точка точка 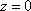 является является?) устранимой ?) точкой ветвления ?) существенной особой точкой ?) полюсом Вопрос id:775567 Для функции 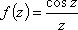 точка точка 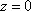 является является?) полюсом ?) существенной особой точкой ?) устранимой ?) неизолированной особой точкой Вопрос id:775568 Для функции 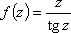 точка точка 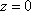 является является?) полюсом ?) устранимой ?) существенной особой точкой ?) точкой ветвления |
Copyright tests.ithead.ru 2013-2026