Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийМатематика (курс 11)Вопрос id:775781 Ряд 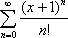 по признаку Даламбера по признаку Даламбера?) расходится при любых  ?) сходится при 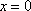 ?) сходится при любых  ?) сходится при 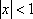 Вопрос id:775782 Ряд 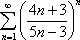 ?) условно сходится ?) сходится ?) абсолютно сходится ?) расходится Вопрос id:775783 Ряд называется сходящимся, если ?) 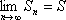 ?) 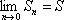 ?) 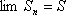 ?) 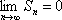 Вопрос id:775784 Ряд Фурье функции 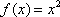 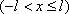 , , 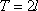 , в точке , в точке 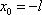 сходится к значению сходится к значению?) 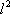 ?) расходится в точке 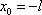 ?) 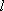 ?) 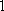 Вопрос id:775785 Рядом Тейлора называется ряд ?) 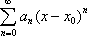 ?) 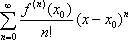 ?) 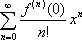 ?) 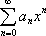 Вопрос id:775786 Ряды 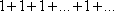 и и 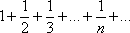 ?) первый - расходится, второй - сходится ?) оба сходятся ?) первый - сходится, второй - расходится ?) оба расходятся Вопрос id:775787 Ряды 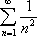 и и 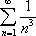 ?) первый - сходится, второй - расходится ?) оба расходятся ?) первый - расходится, второй - сходится ?) оба сходятся Вопрос id:775788 Система линейных уравнений 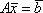 записана в виде, удобном для итераций, если она имеет вид записана в виде, удобном для итераций, если она имеет вид?) 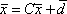 ?) 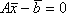 ?) 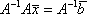 ?) 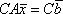 Вопрос id:775789 Согласно теореме Лиувилля функция 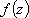 постоянна, если она постоянна, если она?) дифференцируема в смысле R2 в плоскости С и ограничена ?) аналитична в плоскости С и ограничена ?) аналитична в плоскости С ?) ограничена в плоскости С Вопрос id:775790 Согласно теореме о полной сумме вычетов имеет место равенство (  - конечные изолированные особые точки функции - конечные изолированные особые точки функции 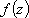 ): ):?) 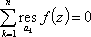 ?) 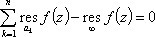 ?) 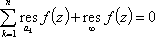 ?) 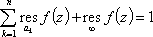 Вопрос id:775791 Спектр линейного оператора А в евклидовом пространстве R2 A = 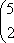 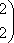 : :?) {  ; 1} ; 1}?) {-1;-  } }?) {-6;-1} ?) {1;6} Вопрос id:775792 Спектр линейного оператора А в евклидовом пространстве R2 A = 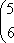 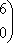 : :?) {-0,25;  } }?) {-  ; 0,25} ; 0,25}?) {-4;9} ?) {-9;4} Вопрос id:775793 Спектр линейного оператора А в евклидовом пространстве R2 A = 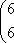 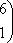 : :?) {-0,1;  } }?) {-10;3} ?) {-3;10} ?) {-  ; 0,1} ; 0,1}Вопрос id:775794 Спектр линейного оператора А в евклидовом пространстве R2 A = 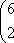 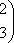 : :?) {-0,5;  } }?) {  ; 0,5} ; 0,5}?) {2;7} ?) {-7;-2} Вопрос id:775795 Спектр линейного оператора А в евклидовом пространстве R2 A= 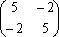 ?) {-  ; ;  } }?) {  ; ;  } }?) {-7;-3} ?) {3;7} Вопрос id:775796 Сходимость итерационного метода решения систем линейных уравнений зависит от ?) величины правых частей системы ?) начального приближения системы ?) вида матрицы системы ?) количества нулей в матрице Вопрос id:775797 Сходится ряд ?) 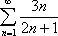 ?) 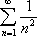 ?) 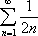 ?) 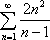 Вопрос id:775798 Сходящимся является знакочередующийся ряд ?) 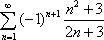 ?) 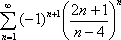 ?) 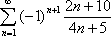 ?) 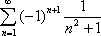 Вопрос id:775799 Теорема Абеля показывает, что для ряда 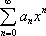 все точки сходимости расположены все точки сходимости расположены?) дальше от начала координат, чем точки расходимости ?) на положительной части числовой оси ?) на всей числовой оси ?) ближе к началу координат, чем точки расходимости Вопрос id:775800 Точка х ∈ А называется предельной для подмножества В Í А, если любая e-окрестность точки х содержит точку множества В, отличную от точки х. Тогда множеством предельных точек множества решений неравенства ex + 3x2y4 > 1 является множество решений ?) ex + 3x2y4 ≤ 1 ?) ex + 3x2y4 ≥ 1 ?) ex + 3x2y4 = 1 ?) ex + 3x2y4 < 1 Вопрос id:775801 Уравнение x(t) - 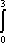 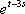 x(s)ds = et является интегральным уравнением x(s)ds = et является интегральным уравнением?) Вольтерра второго рода ?) Вольтерра первого рода ?) Фредгольма второго рода ?) Фредгольма первого рода Вопрос id:775802 Уравнение x(t) - 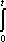 cos(t-s)x(s)ds = lnt является интегральным уравнением cos(t-s)x(s)ds = lnt является интегральным уравнением?) Фредгольма второго рода ?) Фредгольма первого рода ?) Вольтерра второго рода ?) Вольтерра первого рода Вопрос id:775803 Уравнение 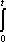 (2t2 - sins)x(s)ds = tgt является интегральным уравнением (2t2 - sins)x(s)ds = tgt является интегральным уравнением?) Фредгольма второго рода ?) Вольтерра первого рода ?) Вольтерра второго рода ?) Фредгольма первого рода Вопрос id:775804 Уравнение 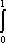 ( t6+s6)x(s)ds = sint является интегральным уравнением ( t6+s6)x(s)ds = sint является интегральным уравнением?) Вольтерра первого рода ?) Фредгольма второго рода ?) Фредгольма первого рода ?) Вольтерра второго рода Вопрос id:775805 Уравнение 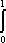 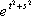 x(s)ds = 2t2 является интегральным уравнением x(s)ds = 2t2 является интегральным уравнением?) Фредгольма первого рода ?) Вольтерра первого рода ?) Фредгольма второго рода ?) Вольтерра второго рода Вопрос id:775806 Уравнение записано в виде, удобном для итераций x=0,5cos2x + π ∕ 8 . Первое приближение метода простой итерации x1 для начального приближения x0=π ∕ 4 равно ?) π ∕ 8 ?) 3π ∕ 4 ?) 3π ∕ 8 ?) π ∕ 4 Вопрос id:775807 Уравнение х(t) - 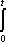 ln(t2s - s3)x(s)ds = et является интегральным уравнением ln(t2s - s3)x(s)ds = et является интегральным уравнением?) Фредгольма первого рода ?) Фредгольма второго рода ?) Вольтерра первого рода ?) Вольтерра второго рода Вопрос id:775808 Уравнение х(t) - 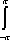 cos(t+2s)x(s)ds = cos2t является интегральным уравнением cos(t+2s)x(s)ds = cos2t является интегральным уравнением?) Фредгольма первого рода ?) Вольтерра первого рода ?) Фредгольма второго рода ?) Вольтерра второго рода Вопрос id:775809 Условие 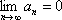 является является?) необходимым признаком сходимости ряда ?) необходимым признаком расходимости ряда ?) необходимым и достаточным признаком сходимости ряда ?) достаточным признаком сходимости ряда Вопрос id:775810 Условия Коши-Римана комплексной дифференцируемости функции 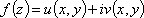 имеют вид имеют вид?) 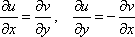 ?) 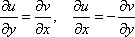 ?) 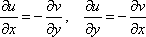 ?) 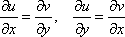 Вопрос id:775811 Формула метода Ньютона для нелинейного уравнения F( x ) = 0 имеет вид: ?) 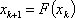 ?) 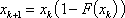 ?) 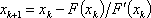 ?) 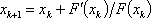 Вопрос id:775812 Формула Муавра имеет вид ?) 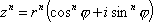 ?) 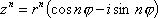 ?) 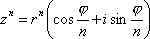 ?) 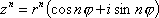 Вопрос id:775813 Функциональный ряд 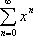 ?) сходится при 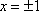 ?) расходится при 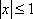 ?) сходится при 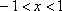 ?) сходится при 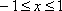 Вопрос id:775814 Функциональный ряд 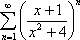 в точках в точках?) 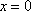 , , 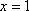 и и 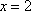 - сходится - сходится?) 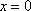 , , 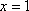 и и 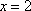 - расходится - расходится?) 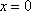 - сходится, - сходится, 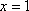 и и 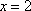 - расходится - расходится?) 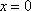 и и 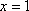 - сходится, - сходится, 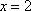 - расходится - расходитсяВопрос id:775815 Функциональным является ряд ?) 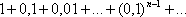 ?) 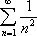 ?) 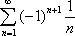 ?) 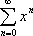 Вопрос id:775816 Функция 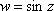 преобразует полуполосу преобразует полуполосу 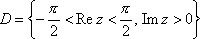 в в?) плоскость w с выброшенной положительной полуосью ?) плоскость w с выброшенным отрезком 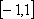 ?) внутренность единичного круга ?) верхнюю полуплоскость Вопрос id:775817 Функция 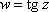 аналитична всюду в С, кроме точек аналитична всюду в С, кроме точек?) 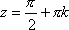 (k - целое) (k - целое)?) 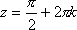 (k - целое) (k - целое)?) 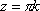 (k - целое) (k - целое)?) 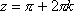 (k - целое) (k - целое)Вопрос id:775818 Функция 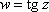 преобразует полосу преобразует полосу 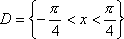 в в?) верхнюю полуплоскость ?) внутренность единичного круга ?) плоскость w с выброшенным отрезком 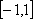 ?) внешность единичного круга Вопрос id:775819 Функция 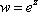 преобразует полосу преобразует полосу 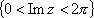 в в?) нижнюю полуплоскость ?) верхнюю полуплоскость ?) плоскость w с выброшенной положительной полуосью ?) плоскость w Вопрос id:775820 Функция 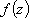 называется аналитической в точке называется аналитической в точке 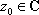 , если она дифференцируема в смысле , если она дифференцируема в смысле?) С в этой точке ?) 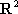 в этой точке в этой точке?) С в некоторой окрестности этой точки ?) 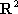 в некоторой окрестности этой точки в некоторой окрестности этой точкиВопрос id:775821 Функция 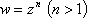 преобразует сектор преобразует сектор 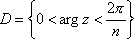 в в?) плоскость w с выброшенным отрезком 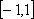 ?) плоскость w с выброшенной положительной полуосью ?) верхнюю полуплоскость ?) плоскость w Вопрос id:775822 Функция 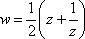 преобразует внешность единичного круга в преобразует внешность единичного круга в?) плоскость w с выброшенной положительной полуосью ?) верхнюю полуплоскость ?) плоскость w с выброшенным отрезком 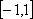 ?) плоскость w с выброшенной отрицательной полуосью Вопрос id:775823 Функция Жуковского - это функция вида ?) 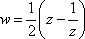 ?) 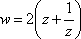 ?) 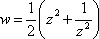 ?) 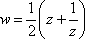 Вопрос id:775824 Частным комплексных чисел 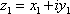 и и 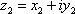 называется число вида называется число вида?) 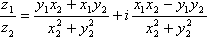 ?) 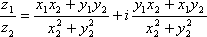 ?) 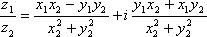 ?) 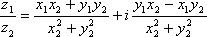 Вопрос id:775825 Число 125,7 в ЭВМ для режима с плавающей точкой в нормализованном виде имеет следующее представление ?) 1,257∙102 ?) 125,7 ?) 0,01257∙104 ?) 0,1257∙103 Вопрос id:775826 Если j(х) является отображением отрезка [a,b] в себя и имеет непрерывную производную j'(х) на отрезке [a,b], то коэффициент сжатия оценивается по формуле q = 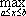 êj'(х) ê . Тогда отображение j(х) = х2 отрезка [-0,4 ; 0,3] в себя является сжатым с коэффициентом сжатия êj'(х) ê . Тогда отображение j(х) = х2 отрезка [-0,4 ; 0,3] в себя является сжатым с коэффициентом сжатия?) -0,8 ?) 0,6 ?) 0,16 ?) 0,8 Вопрос id:775827 Интегральное уравнение Фредгольма x(t) - l 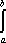 K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при l < K(t,s)x(s)ds = y(t) c параметром l решается методом последовательных приближений при l < 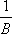 , где В = , где В = 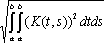 . Тогда интегральное уравнение Фредгольма x(t) - l . Тогда интегральное уравнение Фредгольма x(t) - l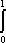 (ts)3 x(s) ds = y(t) решается методом последовательных приближений при l, меньшем (ts)3 x(s) ds = y(t) решается методом последовательных приближений при l, меньшем?) 9 ?) 7 ?) 6 ?) 8 Вопрос id:775828 Расстояние от f(x) до g(x) в пространстве С [a,b] определяется по формуле: r(f(x),g(x)) = 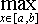 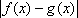 Тогда расстояние между х3 + 3х2 + 1 и 24х в С [0,3] равно Тогда расстояние между х3 + 3х2 + 1 и 24х в С [0,3] равно?) 17 ?) 15 ?) 27 ?) 35 Вопрос id:775829 Расстояние от f(x) до g(x) в пространстве С [a,b] определяется по формуле: r(f(x),g(x)) = 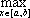 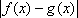 Тогда расстояние между 2х3 + 2 и 3x2 + 12х в С[-1,3] равно Тогда расстояние между 2х3 + 2 и 3x2 + 12х в С[-1,3] равно?) 9 ?) 19 ?) 8 ?) 18 Вопрос id:775831 Бесконечно малые 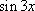 и и  при при 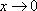 являются являются?) одного порядка малости ?) 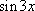 более высокого порядка малости, чем более высокого порядка малости, чем  ?)  более высокого порядка малости, чем более высокого порядка малости, чем 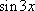 ?) эквивалентными |
Copyright tests.ithead.ru 2013-2026