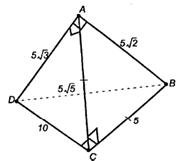
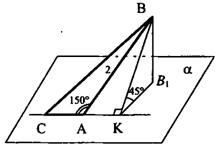
Список вопросов базы знаний

Площадь S(x) круга, по которому плоскость, параллельная плоскости, проходящей через центр и проходящая от нее на расстоянии х < R, пересекает шар, равна

Площадь S_п боковой поверхности призмы выражается равенством: S_n = ___, где Р_n - периметр основания призмы

Площадь S области на сфере радиусом R и объем шарового сектора, основанием которого служит данная область, связаны формулой: V =___

Площадь s(Q) двуугольника Q вычисляется по формуле: S(Q)= ___, где - угол двуугольника (измеряется в радианах)

Площадь s(T) сферического треугольника T, лежащего на сфере S радиусом R, выражается через углы a, b, g этого треугольника по формуле: s(T)= ___

Площадь ___ радиусом R выражается формулой: S =

Площадь боковой поверхности Sп пирамиды выражается формулой: ___, где Рп - периметр основания пирамиды

Площадь боковой поверхности конуса вращения с образующей L и радиусом основания R выражается формулой: S = ___

Площадь боковой поверхности усеченного конуса вращения с радиусами оснований R и r и длиной образующей L выражается формулой: S = ___

Площадь боковой поверхности цилиндра вращения с высотой Н и радиусом основания R выражается формулой: S = ___

Площадь простого многоугольника Р на сфере радиусом R и поворот его границы связаны равенством: s(P)= ___, где - поворот границы многоугольника Р

Площадь сферы радиусом R выражается формулой: S =___

Площадь фигуры, вырезаемой на сфере данным конусом лучей с вершиной в центре сферы и телесным углом w, равна S = ___

Полный телесный угол равен

Полный угол вокруг точки на плоскости равен

При подобных преобразованиях линейные размеры фигур умножаются на ___ подобия

При подобных преобразованиях площади фигур умножаются на ___ подобия

Роль прямых на сфере играют

Свойство, заключающееся в том, что для любых векторов , и (+)´=´ + ´называется

Свойство, заключающееся в том, что для любых векторов и и любого числа х: (x)´=x(´) называется ___

Сложение векторов и умножение вектора на число составляют основу векторной ___ - раздела математики, изучающего векторы

Сумма квадратов ___ параллелограмма равна сумме квадратов всех его сторон

Сумма плоских углов любого выпуклого многогранного угла

Сумму двух векторов можно найти по правилу

Теорема ___ о неизгибаемости замкнутых выпуклых поверхностей при условии, что сохраняется выпуклость поверхности, нашла свои применения в теории оболочек

Точка О, являющаяся центром масс тетраэдра, делит все отрезки, соединяющие вершины тетраэдра с центрами масс противоположных граней в отношении

Угол j между двумя кривыми на поверхности, исходящими из одной точки можно определить по формуле: ___, где l - длина дуги окружности, r - радиус окружности, (если этот предел существует)

Угол между двумя кривыми на поверхности, исходящими из одной точки, определяется обычно как угол между ___ к этим кривым в этой точке (если они существуют)

Числовые коэффициенты x, y, z в равенстве = x + y + z называются ___ вектора в данном базисе

Верны ли утверждения?

А) Если прямая перпендикулярна к прямой, лежащей в плоскости, то она перпендикулярна этой плоскости

В) Через любую точку пространства проходит только одна плоскость, перпендикулярная к данной прямой

Верны ли утверждения?

А) Все прямые, перпендикулярные данной плоскости и пересекающие данную прямую, лежат в одной плоскости

В) Перпендикуляр, проведенный из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости

Параллельные прямые b и с лежат в плоскости α, а прямая а перпендикулярна к прямой b. Верны ли утверждения?

А) прямая а перпендикулярна к прямой с

В) прямая а пересекает плоскость α

Верны ли утверждения?

А) Плоскость и не лежащая в ней прямая, перпендикулярные к одной и той же плоскости, параллельны?

В) Если плоскости α и β пересекаются по прямой а и перпендикулярны к плоскости γ, то прямая а параллельна плоскости γ

Верны ли утверждения?

А) Плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей

В) Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна его граням

В тетраэдре ABCD углы DAB, DAC и АСВ прямые, АС= СВ=5, DB=5. Двугранный угол ABCD равен ___ ^о

Дано: ∆АВС, АС лежит в плоскости α, АВ=2, ВАС=150^о, двугранный угол ВАСВ₁ равен 45^о. Найти расстояние от прямой АС до точки В.

Боковая поверхность правильной треугольной призмы равна 27 см², а полная поверхность - 36 см². Чему равна высота призмы?

Боковое ребро правильной четырехугольной пирамиды равно т и составляет с плоскостью основания угол φ. Найдите объем пирамиды

В тетраэдре KLMN постройте сечение плоскостью, проходящей через ребро KL и середину А ребра MN. Точки Е, О, F – середины отрезков LM, МА и МК. Площадь треугольника EOF равна 12 см². Чему равна площадь треугольника LKA ?

В треугольнике АВС С=90^о, АС=12 см, ВС=16 см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС. СК=24 см. КМ=___ см

Высота пирамиды h=1 м, а основанием служит треугольник АВС, в котором АВ=14 см, ВС=12 см, АВС=30°, объем пирамиды равен ___ см³

Высота правильной усеченной пирамиды равна 2 см, а стороны оснований 1 см и 4 см. Площадь диагонального сечения пирамиды равна ___ см²

Высота правильной усеченной пирамиды равна см, а стороны оснований 3 см и 7 см. Площадь диагонального сечения пирамиды равна ___ см²

Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости α, а катет наклонен к этой плоскости под углом 30°. Угол между плоскостью α и плоскостью треугольника равен ___ ^о

Дано: ∆АВС, С=90^о, А=30^о, АС=а, DCABC, DC =. Угол между плоскостями АDB и АСВ равен ___^о

Как изменится объем правильной пирамиды, если ее высоту увеличить в п раз, а сторону основания уменьшить в п раз? (Пусть V - объем исходной пирамиды, V₁ – объем полученной пирамиды)

Катет АС прямоугольного треугольника ABC с прямым углом С лежит в плоскости α, а угол между плоскостями α и ABC равен 60°. АС = 5 см, АВ = 13 см. Расстояние от точки В до плоскости α равно___

Могут ли две различные плоскости иметь только одну общую точку? (да/нет)

Наибольшая диагональ правильной шестиугольной призмы равна 8 см и составляет с боковым ребром угол в 30°. Объем призмы равен ___ см³

Найдите объем наклонной призмы, у которой основанием является треугольник со сторонами 10 см, 10 см и 12 см, а боковое ребро, равное 8 см, составляет с плоскостью основания угол в 60°