Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийМетоды оптимизации (курс 1)Вопрос id:884322 Минимальное значение функции y=0.5x2 - 3x - 1 на отрезке [0,1] достигается в точке ?) 1 ?) 1/2 ?) 1/3 ?) 0 Вопрос id:884323 Минимальное значение функции y=x2 - 2x + 1 на отрезке [0,1] равно ?) 0.25 ?) 0 ?) 0.5 ?) 1 Вопрос id:884324 Минимальное значение функции y=x2 - 2x - 1 на отрезке [0,1] достигается в точке ?) 0 ?) 1 ?) 1/2 ?) 1/3 Вопрос id:884325 Минимальное значение функции y=x2 - x + 1 на отрезке [0,1] равно ?) 0.75 ?) 1 ?) 0.5 ?) 0.25 Вопрос id:884326 Минимальное значение функции y=x2 - x - 1 на отрезке [0,1] достигается в точке ?) 1/3 ?) 0 ?) 1/2 ?) 1 Вопрос id:884327 Наиболее распространенные методы оптимизации используют понятие ?) системного подхода ?) минимума (или максимум функции или функционала ?) функциональной экстремали ?) среднеквадратичного критерия оптимизации Вопрос id:884328 Не очень строго функционал можно определить как ?) функцию от функции ?) корень алгебраического уравнения ?) производную некоторой функции ?) вариацию некоторой функции Вопрос id:884329 Необходимость требования, чтобы переходный процесс заканчивался в минимальное время, заключается в том, что до окончания переходного процесса система ?) накапливает ошибку рассогласования ?) обладает максимальной степенью неопределенности ?) не реагирует на сигналы-корреляторы ?) не может выполнить своего основного назначения Вопрос id:884330 Необходимым условием существования локального экстремума функции одной переменной является ?) ограниченность функции ?) обращение в ноль ее второй производной ?) обращение в ноль ее первой производной ?) обращение функции в ноль Вопрос id:884331 Неприменимость классических методов вариационного исчисления к некоторым типам разрывных и ступенчатых функций привело к необходимости разработки методов оптимизации типа методов ?) Стильтьеса, Кауфмана ?) Больцано, Коши ?) Беллмана, Понтрягина ?) Эйлера, Лагранжа Вопрос id:884332 Общий вид уравнения Эйлера следующий ?) 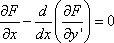 ?) 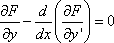 ?) 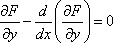 ?) 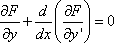 Вопрос id:884333 Одна из основных задач автоматизированных информационных систем (АИуправления - оперативно-календарное планирование, относится к задачам ?) теории принятия решений ?) теории игр ?) классического вариационного исчисления ?) целочисленного программирования Вопрос id:884334 Одним из вариантов записи уравнения Эйлера может быть следующий ?) 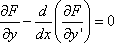 ?) 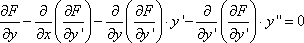 ?) 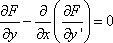 ?) 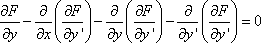 Вопрос id:884335 Оптимальная система управления может быть реализована в виде ?) стратегии или способа управления объектом ?) системы оптимальных критериев ?) стохастического регулирующего механизма ?) системы оптимизационных сигналов Вопрос id:884336 Оптимизация - это ?) процесс нахождения наилучшего решения задачи по некоторому критерию ?) выбор некоторого критерия оптимизации из нескольких возможных ?) определение целевого функционала ?) свойство сложных систем управления Вопрос id:884337 Переходный процесс в теории регулирования - это ?) переходы системы из одного состояния в другое под действием случайных факторов ?) процесс перехода системы в новое качественное состояние ?) процесс возвращения системы к исходному состоянию, после окончания действия возмущения ?) процесс раздвоения фазовой траектории Вопрос id:884338 Постановка задачи оптимизации предполагает наличие ?) системы оптимальных процедур ?) метода расчета критерия оптимизации ?) оптимизирующей процедуры ?) объекта оптимизации и цели оптимизации Вопрос id:884339 Прагматические критерии оптимизации - это ?) выработанные практикой количественные характеристики оптимальности некоторой системы ?) критерии, получаемые на основе решения уравнения Эйлера ?) критерии, полученные на основе математических расчетов ?) специальные критерии, используемые при расчетах строительных конструкций Вопрос id:884340 Примером критерия среднего квадрата ошибки является ?) величина дисперсии разности опорного и выходного сигналов системы ?) коэффициент корреляции между опорным и выходным сигналами ?) величина дисперсии выходного сигнала ?) величина выходного сигнала системы Вопрос id:884341 Примером функционала может служить выражение ?)  ?)  ?)  ?)  Вопрос id:884342 Примером функционала может является ?) определенный интеграл от функции ?) множество ?) дифференциал ?) вариация Вопрос id:884343 Примером функционала может являться ?) сопоставление каждой функции ее максимального значения на отрезке ?) дифференциал функции ?) алгебраическое уравнение ?) вариация функции Вопрос id:884344 Принцип Гамильтона в классической механике формулируется так ?) система движется между двумя точками в фазовом пространстве по такой траектории, для которой некоторый интегральный функционал, называемый действием, обращается в минимум ?) система движется между двумя точками в фазовом пространстве по кратчайшей траектории ?) система движется между двумя точками в фазовом пространстве так, чтобы время движения было минимальным ?) система движется между двумя точками в фазовом пространстве по такой траектории, для которой некоторый интегральный функционал, называемый действием, сохраняет постоянное значение Вопрос id:884345 Принцип Гамильтона в механике формулируется следующим образом: фазовая траектория системы ?) носит колебательный характер ?) является экстремалью функционала ?) ограничена ?) замкнута Вопрос id:884346 Принцип оптимальности Беллмана можно сформулировать так: ?) оптимальная траектория состоит из частей-траекторий, каждая из которых не является оптимальной ?) оптимальная траектория состоит из частей-траекторий, каждая из которых оптимизируется собственным функционалом для соответствующей конечной и начальной точки ?) оптимальная траектория состоит из частей-траекторий, начальная и конечная из которых оптимизируется собственным функционалом для соответствующей конечной и начальной точки ?) оптимальная траектория является единой траекторией, оптимизируемой соответствующим функционалом Вопрос id:884347 Принцип оптимальности Беллмана является основой программирования ?) сепарабельного ?) логического ?) линейного ?) динамического Вопрос id:884348 Принцип оптимальности динамического программирования утверждает, что ?) на оптимальной траектории все участки оптимальны ?) на оптимальной траектории оптимальны 1-й и последний участки ?) если вся траектория оптимальна, то последний участок тоже оптимален ?) если оптимальны 1-й и 2-й участки, то вся траектория оптимальна Вопрос id:884349 Принцип оптимальности справедлив для процессов управления ?) только непрерывных ?) дискретных, и непрерывных ?) только стохастических ?) только дискретных Вопрос id:884350 Принципу оптимальности Беллмана не соответствует формулировка ?) оптимальное управление в любой момент времени будет зависеть от того, как система управлялась, до данного момента ?) начиная с любого промежуточного момента времени, участок оптимальной траектории также оптимален ?) оптимальное управление в любой момент времени не зависит от предыстории системы ?) если управление оптимально, то каково бы не было начальное состояние системы и управление в начальный момент, последующее управление оптимально относительно состояния на данный момент Вопрос id:884351 Приращением или вариацией dy аргумента y(x) функционала J(y(x)) называется ?) разность между двумя функциями dy=y(x) - y0(x) ?) частное двух функций dy=y(x) и y0(x) ?) произведение двух функций dy=y(x) и y0(x) ?) сумма двух функций dy=y(x) + y0(x) Вопрос id:884352 Пусть задан функционал I(y(x)+eh(x)) (e-число), тогда 1-й вариацией функционала является выражение ?)  ?)  ?)  ?)  Вопрос id:884353 Пусть задан функционал I(y(x)+eh(x)) (e-число), тогда 2-й вариацией функционала является выражение ?)  ?)  ?)  ?)  Вопрос id:884354 С геометрической точки зрения вариационная задача  с подвижными концами состоит в определении кривой с подвижными концами состоит в определении кривой?) концы которой проходят через заданные точки ?) имеющей конечное число точек разрыва ?) концы которой расположены на вертикальных прямых х=а и х=b ?) концы которой расположены на горизонтальных прямых y=а и y=b Вопрос id:884355 С геометрической точки зрения особенностью вариационных задач с подвижными границами является то, что область определения допустимых функций ?) ограничена положительными значениями х ?) ограничена отрицательными значениями х ?) фиксирована ?) не фиксирована, а меняется от функции к функции Вопрос id:884356 Среди следующих утверждений верным является утверждение, что ?) у функции, непрерывной в замкнутом интервале и принимающей на концах значения разных знаков, 2-я производная, по меньшей мере, один раз обращается в ноль внутри интервала ?) функция, непрерывная в замкнутом интервале и принимающая на его концах значения разных знаков, по меньшей мере, один раз обращается в ноль внутри интервала ?) у функции, непрерывной в замкнутом интервале и принимающей на концах значения разных знаков, 1-я производная, по меньшей мере, один раз обращается в ноль внутри интервала ?) функция, непрерывная в замкнутом интервале и принимающая на его концах значения разных знаков, по меньшей мере, два раза обращается в ноль внутри интервала Вопрос id:884357 Стоимость функционирования системы массового обслуживания в единицу времени можно определить как ?) C = c1pcp - c2wcp , ?) C = c1pcp + c2wcp , ?) C = c1 + c2 , ?) C = pcp + wcp , Вопрос id:884358 Точкой бесконечного разрыва функции называется точка, в которой ?) функция при подходе к точке разрыва стремятся к бесконечности ?) 2-я производная стремится к бесконечности ?) функция имеет правый и левый пределы не равные между собой ?) 1-я производная стремится к бесконечности Вопрос id:884359 Точкой разрыва функции 1-го рода называется точка, в которой функция имеет ?) правый и левый пределы равные между собой ?) правый и левый пределы не равные между собой ?) разрыв 2-й производной ?) разрыв 1-й производной Вопрос id:884360 Точкой устранимого разрыва функции называется точка, в которой функция имеет ?) правый и левый пределы не равные между собой ?) разрыв 2-й производной ?) разрыв 1-й производной ?) правый и левый пределы равные между собой Вопрос id:884361 Уравнение Эйлера для функционала  имеет вид имеет вид?)  ?)  ?)  ?)  Вопрос id:884362 Уравнение Эйлера служит для нахождения экстремума функционала вида ?)  ?)  ?)  ?)  Вопрос id:884363 Уравнения Гамильтона для функционала  являются другой формой записи являются другой формой записи?) условий трансверсальности ?) уравнения Эйлера ?) дополнительных ограничений на функцию ?) дополнительных ограничений на функцию и ее производную Вопрос id:884364 Уравнения Гамильтона представляют собой систему ?) двух дифференциальных уравнений 1-го порядка ?) трех дифференциальных уравнений 1-го порядка ?) двух алгебраических уравнений ?) двух дифференциальных уравнений 2-го порядка Вопрос id:884365 Условие Лежандра позволяет ?) определять знаки второй производной ?) отличать минимум от максимума ?) определять знак первой вариации ?) находить экстремаль вырожденного функционала Вопрос id:884366 Условия трансверсальности возникают в вариационной задаче, когда ?) функция имеет разрыв первого рода ?) концы искомой функции свободны ?) концы искомой функции неподвижно закреплены ?) концы искомой функции могут перемещаться по заданным кривым Вопрос id:884367 Функционал J(y(x)) называется непрерывным, если малому изменению ?) y’(x) соответствует малое изменение J(y(x)) ?) x соответствует малое изменение J(y(x)) ?) y(x) соответствует малое изменение J(y(x)) ?) y’’(x) соответствует малое изменение J(y(x)) Вопрос id:884368 Функционал J(y) называется линейным, если для любых чисел a1 и a2 выполняется условие: ?) J[a1y1 + a2y2]= a1a2J[y1 + y2] ?) J[a1y1 + a2y2]= a1J[y1] + a2J[y2] ?) J[a1y1 + a2y2]= a1J[y1] x a2J[y2] ?) J[a1y1 + a2y2]= (a1 + a2 )J[y1 + y2] Вопрос id:884369 Функциональное уравнение Беллмана представляет собой ?) гамильтониан ?) подкласс уравнения Эйлера ?) формальную запись принципа оптимальности ?) подкласс обобщенного уравнения Лежандра Вопрос id:884370 Функция  имеет в нуле точку имеет в нуле точку?) бесконечного разрыва ?) непрерывности функции ?) разрыва 1-го рода ?) устранимого разрыва Вопрос id:884371 Функция f(x) имеет на отрезке [a,b] глобальный минимум в точке x*, если ?) для всех xÎ[a,b] f(x*)³f(x) ?) f(x*)=0 ?) для всех xÎ[a,b] f(x*)£f(x) ?) f(x) ограничена на [a,b] |
Copyright tests.ithead.ru 2013-2026