Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийАлгебра и геометрия (курс 3)Вопрос id:634256 Вычислите сумму элементов первого столбца матрицы 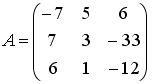 , ,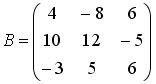 Вопрос id:634257 Вычислите сумму элементов первого столбца матрицы 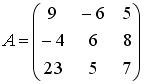 , ,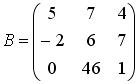 Вопрос id:634258 Вычислите сумму элементов первого столбца матрицы 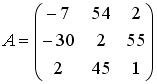 , ,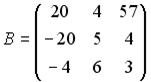 Вопрос id:634259 Горловым сечением однополосного гиперболоида x2 + y2 – z2 – 4x = 0 является ?) эллипс с центом (0,0,0) и полуосями a = 1, b = 2 ?) окружность с центом (0,0,0) и радиусом R = 4 ?) окружность с центом (2,0,0) и радиусом R = 2 ?) эллипс с центом (2,0,0) и полуосями a = 2, b = 1 Вопрос id:634260 Дана матрица 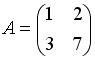 . Тогда элемент второй строки первого столбца матрицы . Тогда элемент второй строки первого столбца матрицы ?) 2 ?) -2 ?) -3 ?) 3 Вопрос id:634261 Дана матрица 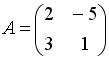 . Тогда алгебраическим дополнением элемента . Тогда алгебраическим дополнением элемента ?) – 1 ?) 3 ?) – 5 ?) 5 Вопрос id:634262 Дана матрица 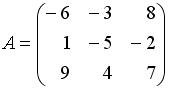 , тогда сумма , тогда сумма ?) 5 ?) – 9 ?) – 6 ?) – 5 Вопрос id:634312 Дана матрица 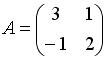 . Тогда элемент . Тогда элемент ?) - 1 ?) - 5 ?) 1 ?) 5 Вопрос id:634394 Дана матрица 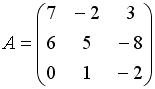 . Тогда алгебраическое дополнение элемента . Тогда алгебраическое дополнение элемента Вопрос id:634480 Дана матрица 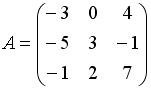 . Тогда алгебраическое дополнение элемента . Тогда алгебраическое дополнение элемента Вопрос id:634557 Дана матрица 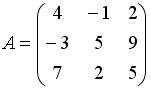 . Тогда алгебраическое дополнение элемента . Тогда алгебраическое дополнение элемента Вопрос id:634718 Дана матрица 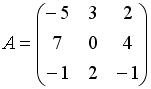 . Тогда алгебраическое дополнение элемента . Тогда алгебраическое дополнение элемента Вопрос id:634720 Дана плоскость 2x + y – 2z + 9 = 0 и точка M(–2,–1,2) ?) точка М не лежит на плоскости ?) точка М является проекцией начала координат на плоскость ?) точка М и начало координат лежат на плоскости ?) точка М отстоит от плоскости на расстоянии 1 Вопрос id:634722 Дана плоскость x + y + z – 6 = 0 и точки M1(1,–1,3) и M2(2,0,4) ?) прямая M1M2 перпендикулярна плоскости ?) точка M1 удалена от плоскости на расстояние d = 1 ?) прямая M1M2 лежит на плоскости ?) прямая M1M2 параллельна плоскости Вопрос id:634723 Дана плоскость x + y + z – 6 = 0 и точки M1(1,–1,3), M2(2,0,4) ?) обе точки лежат на плоскости ?) расстояние от точки M2 до плоскости равно 1 ?) расстояние от точки M2 до плоскости равно 0 ?) прямая M1M2 лежит на плоскости Вопрос id:634725 Дана плоскость x + y + z – 9 = 0 и точка M(3,3,3), тогда ?) точка М и начало координат лежат на плоскости ?) точка М отстоит от плоскости на расстоянии 9 ?) точка М является проекцией начала координат на плоскость ?) точка М не лежит на плоскости Вопрос id:634727 Дана плоскость x + y – z – 6 = 0 ?) плоскость пересекает оси координат в точках M1(6,0,0), M2(0,6,0), M3(0,0,6) ?) плоскость отсекает на координатных осях отрезки равной длины ?) плоскость пересекает оси координат в точках M1(6,0,0), M2(0,–6,0), M3(0,0,–6) ?) плоскость пересекает оси координат в точках M1(–6,0,0), M2(0,–6,0), M3(0,0,6) Вопрос id:634788 Дана прямая
Вопрос id:634830 Дана прямая
Вопрос id:634872 Дана прямая
Вопрос id:634873 Дана система уравнений 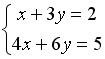 . Для того, чтобы найти значение переменной . Для того, чтобы найти значение переменной ?) ?) ?) ?) Вопрос id:634874 Дана сфера x2 + y2 + z2 – 2x – 8 = 0. Установите верные соответствия между плоскостями и их пересечениями со сферой
Вопрос id:634875 Даны матрицы 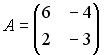 и и 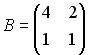 . Тогда определитель произведения матриц . Тогда определитель произведения матриц ?) -20 ?) 0 ?) 18 ?) 6 Вопрос id:634876 Даны матрицы 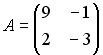 и и 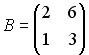 . Тогда определитель произведения матриц . Тогда определитель произведения матриц ?) 3 ?) 0 ?) 2 ?) -3 Вопрос id:634877 Даны матрицы ?) 4 ?) 4 ?) 6 ?) 6 Вопрос id:634878 Даны матрицы 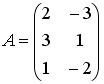 и и 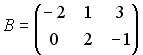 . Тогда матрица . Тогда матрица ?) 3 ?) 2 ?) 3 ?) 2 Вопрос id:634879 Даны матрицы 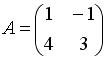 и и 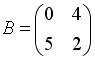 . Тогда решением матричного уравнения . Тогда решением матричного уравнения ?) 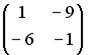 ?) 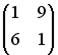 ?) 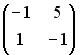 ?) 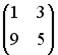 Вопрос id:634880 Даны матрицы 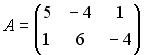 и и 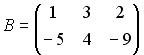 . Тогда матрица . Тогда матрица ?) 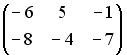 ?) 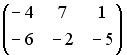 ?) 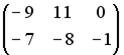 ?) 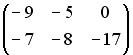 Вопрос id:634881 Даны матрицы 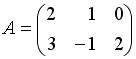 и и 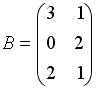 . Сумма элементов матрицы . Сумма элементов матрицы Вопрос id:634882 Даны матрицы 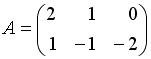 и и 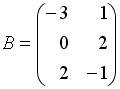 . Сумма элементов матрицы . Сумма элементов матрицы Вопрос id:634883 Даны матрицы 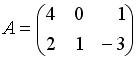 и и 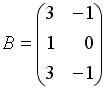 . Сумма элементов матрицы . Сумма элементов матрицы Вопрос id:634884 Даны матрицы 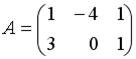 и и 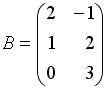 . Сумма элементов матрицы . Сумма элементов матрицы Вопрос id:634885 Даны матрицы 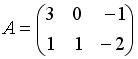 и и 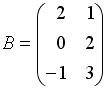 . Сумма элементов матрицы . Сумма элементов матрицы Вопрос id:634886 Даны матрицы 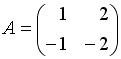 и и 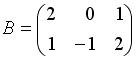 . Сумма элементов матрицы . Сумма элементов матрицы Вопрос id:634887 Даны матрицы 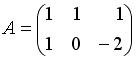 и и 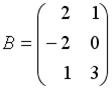 . Сумма элементов матрицы . Сумма элементов матрицы Вопрос id:634888 Даны плоскости 1) 2x + 2y – z + 12 = 0; 2) x – 2y + 2z + 2 = 0; 3) 2x – y + 2z – 6 = 0. С увеличением расстояния от начала координат плоскости располагаются в порядке ?) 1, 2, 3 ?) 2, 3, 1 ?) все плоскости отстоят от начала координат на одинаковом расстоянии ?) 2, 1, 3 Вопрос id:634889 Даны плоскости 1) 2x + 2y – z + 6 = 0, 2) x – 2y + 2z – 6 = 0, 3) 2x + 4y – 4z – 12 = 0. Пусть d1, d2, d3 – расстояния от начала координат до каждой плоскости соответственно. Тогда ?) d1 + d2 = d3 ?) d1 = d2 = d3 ?) d3 = 2d1, d1 = d2 ?) d2 = 2d1, d3 = d2 Вопрос id:634890 Даны плоскости 1) 2x + 6y – 3z + 14 = 0; 2) 3x + 2y – 6z + 21 = 0; 3) 6x + 3y – 2z + 7 = 0. На расстоянии d = 3 от точки M0(0,0,–7) отстоят плоскости ?) 1, 3 ?) никакая ?) 2, 3 ?) 3 Вопрос id:634891 Даны плоскости 1) 2x + y – 2z + 9 = 0 и 2) x – 2y + 2z + 3 = 0. Расстояния d1 и d2 от начала координат до плоскости 1) и 2) соответственно удовлетворяют равенству ?) d1 = d2 ?) d1 = 3d2 ?) ?) d1 = 2d2 Вопрос id:634892 Даны плоскости 1) 6x + 3y – 2z -7 =0; 2) 2x + 6y -3x + 21 =0; 3) 3x + 2y – 6z – 14 = 0. С увеличением расстояния от начала координат плоскости расположены в порядке ?) 1, 2, 3 ?) 1, 3, 2 ?) 3, 1, 2 ?) все плоскости расположены на одинаковом расстоянии Вопрос id:634893 Даны плоскости 1) x + 2y – 2z + 3 = 0 и 2) x + 2y – 2z – 6 = 0 и точка M0(1,1,0) ?) расстояние d1 от M0 до плоскости 1) d1 = 2, а расстояние до плоскости 2) d2 = 1 ?) расстояние от M0 до плоскости 1) вдвое больше, чем до плоскости 2) ?) точка M0 равноудалена от плоскостей 1) и 2) ?) расстояние от M0 до плоскости 1) d1 = 6, а до плоскости 2) d2 = 3 Вопрос id:634894 Даны плоскости 1) x + y + z – 3 = 0; 2) x – y + z + 3 = 0, тогда ?) обе плоскости отстоят от начала координат на равном расстоянии ?) плоскость 1) удалена от начала координат на расстоянии вдвое большем, чем плоскость 2) ?) обе плоскости проходят через начало координат ?) плоскость 1) двое ближе к началу координат, чем плоскость 2) Вопрос id:634895 Даны плоскости
Вопрос id:634896 Даны плоскости: 1) 2x – y + 3z – 2 = 0; 2) 2x – y + 3z + 2 = 0; 3) 2x – y + 3z – 4 = 0; 4) 3x+ y – – 2z + 2 = 0. На одинаковом расстоянии от начала координат находятся плоскости ?) 2, 3, 4 ?) 3, 4 ?) 1, 2, 4 ?) 1, 2, 3 Вопрос id:634897 Даны плоскости: 1) x + 2y – 2z – 4 = 0; 2) x + 2y – 2z + 8 = 0; 3) x + 2y – 2z + 2 = 0 ?) расстояние от плоскости 3) до плоскости 2) вдвое больше расстояния до плоскости 1) ?) расстояние от плоскости 3) до плоскости 2) равно 8 ?) расстояние от плоскости 3) до плоскости 1) равно 2 ?) плоскость 3) равноудалена от плоскостей 1) и 2) Вопрос id:634898 Даны плоскость 2x + 2y – z + 6 = 0 и точки М1(1,1,1) и М2(4,4,4). d1 – расстояние от точки М1 до плоскости, d2 – расстояние от точки М2 до плоскости, тогда ?) d1 = d2 ?) d1 = 3d2 ?) d1 = 2d2 ?) d2 = 2d1 Вопрос id:634899 Даны плоскость 2x + 2y – z + 6 = 0 и точки М1(1,1,1) и М2(4,4,4). Пусть d1 – расстояние от точки М1 до плоскости, d2 – расстояние между точками М1, М2, тогда ?) d1 > d2 ?) d2 = d1 ?) d1 = 4d2 ?) Вопрос id:634900 Даны плоскость 2x + 2y – z + 6 = 0 и точки М1(3,0,3) и М2(7,4,5). Пусть d1 – расстояние от точки М1 до плоскости, d2 – расстояние между точками М1 и М2, тогда ?) d2 = d1 ?) d1 = 2d2 ?) d1 > d2 ?) d2 = 2d1 Вопрос id:634901 Даны прямые ?) прямая L2 лежит в плоскости α, а L1 – пересекает ее ?) прямая L1 лежит в плоскости α, а L2 – пересекает ее ?) обе прямые пересекают плоскость ?) обе прямые L1 и L2 лежат в плоскости α Вопрос id:634902 Даны прямые ?) прямая L1 пересекает плоскость α, L2 – лежит в плоскости ?) обе прямые пересекают плоскость ?) прямая L2 пересекает плоскость, а L2 – лежит в ней ?) прямые L1 и L2 лежат в плоскости α |
Copyright tests.ithead.ru 2013-2026