Вход | Регистрация
Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.

Список вопросов базы знаний

Математика (курс 3)

Вопрос id:740921
Градиент функции Z = f(x, y) в точке P - это вектор
?) указывающий направление наибольшего изменения функции в точке P
?) имеющий модуль, равный значению функции в точке P
?) указывающий направление изменения функции в точке P
?) имеющий модуль, равный скорости изменения функции в точке P
Вопрос id:740922
Дифференциальное уравнение является
?) неоднородным с переменными коэффициентами
?) неоднородным с постоянными коэффициентами
?) однородным с постоянным коэффициентами
?) однородным с переменными коэффициентами
Вопрос id:740923
Дифференциальное уравнение является
?) однородным с переменными коэффициентами
?) однородным с постоянными коэффициентами
?) неоднородным с постоянными коэффициентами
?) неоднородным с переменными коэффициентами
Вопрос id:740924
Для дифференциального уравнения
?) Общее решение
?) Характеристическое уравнение
?) Характеристическое уравнение
?) Общее решение
Вопрос id:740925
Для функции Z = f(x, y) установите соответствие между формулами и их названиями
Левая частьПравая часть
полный дифференциал
производная по направлению
градиент
Вопрос id:740926
Если в точке P0(x0, y0) функция имеет экстремум, то
?) касательная плоскость к поверхности Z = f(p) в точке M0(x0, y0; f(x0, y0)) перпендикулярна оси ОХ
?) касательная плоскость к поверхности Z = f(P) в точке M0(x0, y0; f(x0, y0)) параллельна плоскости OXY или не существует
?) частные производные функции f(x, y) в точке P0 равны нулю или не существуют
?) частные производные функции f(x, y) в точке P0 равны бесконечности
Вопрос id:740927
Задача Коши имеет решение
?)
?) xex
?)
?) 2x
Вопрос id:740928
Задача Коши имеет решение
?) ex
?) xex
?) 2x
?) 2xex
Вопрос id:740929
Задачей Коши является задача
?) нахождение решения дифференциального уравнения
?) нахождение решения дифференциального уравнения, удовлетворяющего начальным условиям
?) нахождение общего решения дифференциального уравнения
?) нахождение общего интеграла дифференциального уравнения
Вопрос id:740930
Корни характеристического уравнение для (наберите числа через запятую)
Вопрос id:740931
Корни характеристического уравнения для равны r1=…, r2=…. (наберите числа через запятую)
Вопрос id:740932
Корни характеристического уравнения для равны (набрать целые числа в порядке возрастания через запятую)
Вопрос id:740933
Корни характеристического уравнения для равны (набрать целые числа в порядке возрастания через запятую)
Вопрос id:740934
Корни характеристического уравнения для равны (набрать целые числа в порядке возрастания через запятую)
Вопрос id:740935
Критическая точка функции Z = f(x, y) имеет координаты P0(x0, y0). Неравенство 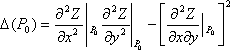> 0 есть ___ условие наличия экстремума (наберите слово)
Вопрос id:740936
Линейным дифференциальным уравнением первого порядка будет уравнение
?)
?)
?)
?)
Вопрос id:740937
Линии уровня для функции z=x2+y2 имеют вид
?) x2+y2 =C
?) x2+y2 =1
?) x2+y2 =C, C<0
?) x2+y2 = C, C≥ 0
Вопрос id:740938
Линии уровня для функции z = ln(x3 - y3) имеют вид
?) x3 - y3 =C
?) x3 - y3 = 1
?) x3 - y3 = C, C > 0
?) x3 - y3 >0
Вопрос id:740939
Линии уровня для функции z = xy2 имеют вид
?) x>0, y>0
?)
?)
?)
Вопрос id:740940
Линия уровня функции z = x2 – y2 в точке P0(1, 0) имеет уравнение
?) x2 – y2 = const
?) 2x - 2y = 1
?) x2 – y2 = 1
?) x2 – y2 = 0
Вопрос id:740941
Область определения функции есть множество
?) {(x,y) : x3 ≠y}
?) вся плоскость XOY, кроме точки O(0,0)
?) {(x,y) : y<x3 }
?) вся плоскость XOY
Вопрос id:740942
Область определения функции есть множество
?) вся плоскость XOY
?) {(x,y): x>0, y>0}
?) {(x,y): -µ<x<µ, -µ<y<µ}
?) вся плоскость XOY, кроме точки О(0,0)
Вопрос id:740943
Область определения функции есть множество
?) вся плоскость XOY, кроме точки O(0,0)
?) {(x,y) : x≥0, y≥0}
?) {(x,y): -µ<x<∞, -∞<y<∞ }
?) {(x,y) : x+y≥0}
Вопрос id:740944
Область определения функции есть множество
?) {(x, y):
?) {(x, y):}
?) {(x, y): }
?) {(x, y):-}
Вопрос id:740945
Область определения функции z = 2x+y есть множество
?) вся плоскость XOY, кроме точки O(0,0)
?) {(x,y) : -∞<x<∞, -∞<y<∞}
?) вся плоскость XOY
?) {(x,y) : x+y>0}
Вопрос id:740946
Область определения функции z= lny есть множество
?) {(x,y) : y>0}
?) {(x,y) : x>0, y>0}
?) {(x,y) : >1}
?) {(x,y) : x≠0, y>0}
Вопрос id:740947
Область определения функции z=есть множество
?) {(x,y) : y≠2x}
?) {(x,y) :вся плоскость XOY, кроме точки O(0,0)
?) {(x,y) : x>0, y>0}
?) {(x,y) : x≠0, y≠0}
Вопрос id:740948
Область определения функции z=есть множество
?) {(x,y) : y>2}
?) {(x,y) : x≠0, y>0}
?) {(x,y) : y<2x}
?) {(x,y) : y≤-2x}
Вопрос id:740949
Область определения функции z=есть множество
?) {(x,y) : x≥0, y≥0}
?) {(x,y) : -µ<x<µ,-µ< y<µ}
?) {(x,y) : x≠0, y≠ }
?) {(x,y) : xy>0}
Вопрос id:740950
Область определения функции z=ln(2x+y) есть множество
?) {(x,y) : y<-2x}
?) {(x,y) : x>0,y>0}
?) {(x,y) : y≥-2x}
?) {(x,y) : y>-2x}
Вопрос id:740951
Общее решение дифференциального уравнения равно
?) 1
?)
?)
?)
Вопрос id:740953
Открытая область D - множество точек на плоскости, обладающей свойствами
?) каждая точка P0(x0, y0) принадлежит множеству D
?) всякие две точки множества можно соединить непрерывной линией
?) каждая точка P0(x0, y0) множества D принадлежит ей вместе с некоторой d - окрестностью точки P0
?) всякие две точки множества можно соединить непрерывной линией, целиком лежащей в D
Вопрос id:740954
Поверхности уровня для функции u = x2 + y2 - z имеют вид
?) x2 + y2 > z
?) x2 + y2 = z
?) x2 + y2 - z = C
?) x2 + y2 - z > 1
Вопрос id:740955
Поверхности уровня для функции u = x2 +y2 +z2 имеют вид
?) x2 +y2 +z2 >0
?) x2 +y2 +z2 = C, C≥0
?) x2 +y2 +z2 =1
?) x2 +y2 +z2 =C
Вопрос id:740956
Поверхности уровня для функции u =x2 yz имеют вид
?) x2 yz>0
?) x2 yz=C, C>0
?) x2 yz=1
?) x2 yz=C
Вопрос id:740958
Поверхностью уровня для функции u = f(x, y, z) называется поверхность, определяемая уравнением
?)
?)
?)
?)
Вопрос id:740959
Полное приращение функции Z = f(x, y) в точке P(x, y) равно
?)
?)
?)
?)
Вопрос id:740960
Полный дифференциал функции Z = 2x2 + 2y2 в точке P0(1, 1) равен
?) 4dx + 4dy
?) 4xdx + 4ydy
?) 2dx + 2dy
?) dx + dy
Вопрос id:740961
Полный дифференциал функции Z = x3 - y3 в точке P0(1, 1) равен
?) 3dx - 3dy
?) 0
?) dx - dy
?) 3dx + 3dy
Вопрос id:740962
Полный дифференциал функции Z = x5 + y5 в точке P0(-1, -1) равен
?) -5dx - 5dy
?) dx + dy
?) -dx - dy
?) 5dx + 5dy
Вопрос id:740963
Полный дифференциал функции равен
?) xdy + ydx
?) (dx dy)
?) (ydx +xdy)
?) (dx +dy)
Вопрос id:740964
Полный дифференциал функции Z = ln(x+y) в точке P0(1, 0) равен
?) dx + dy
?) (dx + dy)/x
?)
?) dx
Вопрос id:740965
Полным дифференциалом функции z =f(x, y) называется выражение
?) f(x, y)dxdy
?)
?)
?)
Вопрос id:740966
Предел функции Z = f(p) = f(x, y)
?)
?)
?)
?)
Вопрос id:740967
Решение задачи Коши равно
?)
?)
?) 2
?)
Вопрос id:740968
Решение задачи Коши равно
?) 1
?)
?)
?)
Вопрос id:740969
Стационарная точка для функции Z = 2xy имеет координаты (___,___) (набрать целые числа через запятую)
Вопрос id:740970
Стационарная точка для функции Z = x2 + 2x - y3 имеет координаты (___,___) (набрать целые числа через запятую)
Вопрос id:740971
Стационарная точка для функции Z = x2 + y2 - 4 имеет координаты (___,___) (набрать целые числа через запятую)
Вопрос id:740972
Стационарная точка для функции Z = x2 + y2 - 6y имеет координаты (___,___) (набрать целые числа через запятую)
Copyright tests.ithead.ru 2013-2026