Список вопросов базы знанийГеометрия (8 кл. БП)Вопрос id:862818 Дан треугольник, стороны которого равны 8 см, 5 см, 7 см. Найдите периметр треугольника, вершинами которого являются середины сторон данного треугольника
?) 10 см ?) 12 см ?) 8 см ?) 9 см Вопрос id:862820 Диагональ АС параллелограмма ABCD равна 18 см. Середина М стороны АВ соединена с вершиной D. Найдите отрезки, на которые делится диагональ АС отрезком DM
?) 3 см, 15 см ?) 6 см, 12 см ?) 5 см, 13 см ?) 4 см, 14 см Вопрос id:862821 Катеты прямоугольного треугольника относятся как 3 : 4, а гипотенуза равна 50 мм. Найдите отрезки, на которые гипотенуза делится высотой, проведенной из вершины прямого угла
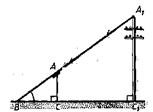
?) 10 мм; 40 мм ?) 12 мм; 38 мм ?) 18 мм; 32 мм ?) 20 мм; 30 мм Вопрос id:862822 Определите высоту телеграфного столба А1С1, изображенного на рисунке, если
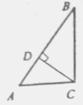
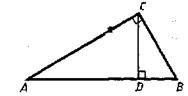
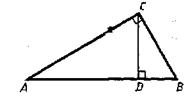
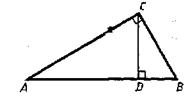
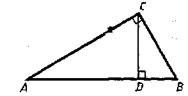
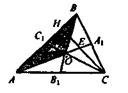
?) 6,5 м ?) 5,1 м ?) 4,2 м ?) 5,5 м Вопрос id:862823 Рассмотрите чертеж.
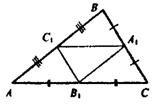
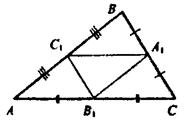
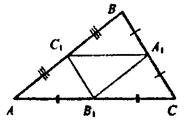
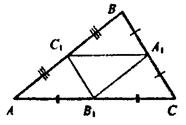
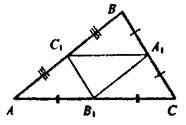
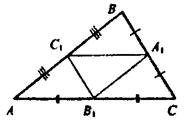
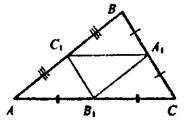
Отметьте верные утверждения: ?) Δ ABC ~ Δ CBD ?) Δ ACD ~ Δ CBD ?) Δ ACD = Δ ABC ?) Δ ABC ~ Δ ACD Вопрос id:862825 Стороны треугольника АВС равны АВ = 12 см, ВС = 14 см и АС = 18 см, А1, В1, С1 – середины его сторон. Сторона А1В1 треугольника А1В1С1 равна ___ (число) см
Вопрос id:862826 Стороны треугольника АВС равны АВ = 12 см, ВС = 14 см и АС = 18 см, А1, В1, С1 – середины его сторон. Сторона А1С1 треугольника А1В1С1 равна ___ (число) см
Вопрос id:862827 Стороны треугольника АВС равны АВ = 12 см, ВС = 14 см и АС = 18 см, А1, В1, С1 – середины его сторон. Сторона В1С1 треугольника А1В1С1 равна ___ (число) см
Вопрос id:862828 Стороны треугольника АВС равны АВ = 8 см, ВС = 10 см и АС = 12 см, А1, В1, С1 – середины его сторон. Сторона А1В1 треугольника А1В1С1 равна ___ (число) см
Вопрос id:862830 Стороны треугольника АВС равны АВ = 8 см, ВС = 10 см и АС = 12 см, А1, В1, С1 – середины его сторон. Сторона А1С1 треугольника А1В1С1 равна ___ (число) см
Вопрос id:862832 Стороны треугольника АВС равны АВ = 8 см, ВС = 10 см и АС = 12 см, А1, В1, С1 – середины его сторон. Сторона В1С1 треугольника А1В1С1 равна ___ (число) см
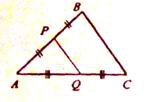
Вопрос id:862833 Точки Р и Q – середины сторон АВ и АС треугольника ABC. Найдите периметр треугольника ABC, если периметр треугольника APQ равен 21 см
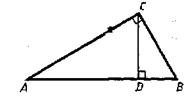
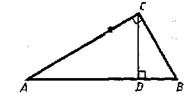
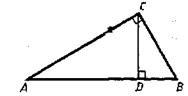
?) 31,5 см ?) 63 см ?) 73,5 см ?) 42 см Вопрос id:862835 В прямоугольном треугольнике ABC с прямым углом С и высотой CD: AD = 25, DB = 16. Найдите катеты треугольника АВС
?) 3 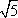 ?) 4 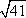 ?) 5 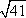 ?) 2 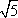 Вопрос id:862841 В прямоугольном треугольнике ABC с прямым углом С и высотой CD: AD = 36, DB = 64. Найдите катеты треугольника АВС:
?) 40 ?) 80 ?) 60 ?) 30 Вопрос id:862846 В прямоугольном треугольнике ABC с прямым углом С и высотой CD: АС = 12, AD = 6. Найдите гипотенузу и другой катет
?) 2 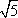 ?) 18 ?) 24 ?) 12 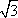 Вопрос id:862863 В прямоугольном треугольнике ABC с прямым углом С и высотой CD: ВС = 6, АВ = 9. Найдите высоту CD и катет AC
?) 2 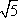 ?) 3 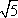 ?) 12 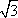 ?) 8 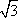 Вопрос id:862878 В прямоугольном треугольнике ABC с прямым углом С и высотой CD: ВС = 6, АВ = 9. Найдите отрезки АD и DB
?) 5 ?) 3 ?) 4 ?) 6 Вопрос id:862879 В прямоугольном треугольнике ABC с прямым углом С и высотой CD: ВС = 8, DB = 4. Найдите гипотенузу АВ и катет АС
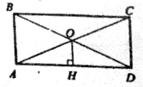
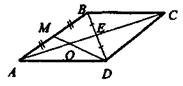
?) 8 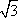 ?) 16 ?) 12 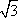 ?) 12 Вопрос id:862892 В треугольнике ABC медианы АА1 и ВВ1 пересекаются в точке О. Найдите площадь треугольника ABC, если площадь треугольника АВО равна S
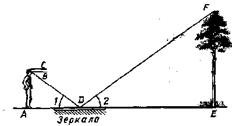
?) 3S ?) 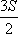 ?) 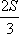 ?)  Вопрос id:862909 Для определения высоты дерева можно использовать зеркало так, как показано на рисунке. Луч света FD, отражаясь от зеркала в точке D, попадает в глаз человека (точку В). Определите высоту дерева, если АС = 165 см, ВС = 12 см, AD = 120 см, DE = 4,8 м,
?) 6,04 м ?) 6,12 м ?) 5,28 м ?) 5,92 м Вопрос id:862919 Расстояние от точки пересечения диагоналей прямоугольника до прямой, содержащей его большую сторону, равно 2,5 см. Найдите меньшую сторону прямоугольника
?) 7,5 см ?) 10 см ?) 6 см ?) 5 см Вопрос id:862920 Высота прямоугольного треугольника, проведенная из вершины прямого угла: ?) есть среднее арифметическое для катетов ?) есть среднее арифметическое для отрезков, на которые гипотенуза делится этой высотой ?) есть среднее пропорциональное для отрезков, на которые гипотенуза делится этой высотой ?) есть среднее геометрическое для катетов ?) делит гипотенузу на отрезки, пропорциональные прилегающим катетам Вопрос id:862926 Катет прямоугольного треугольника есть среднее пропорциональное для ?) другого катета и высоты, проведенной из прямого угла ?) гипотенузы и отрезка гипотенузы, заключенного между катетом и высотой, проведенной из вершины прямого угла ?) гипотенузы и высоты, проведенной из прямого угла ?) гипотенузы и другого катета Вопрос id:862930 Средняя линия любого треугольника параллельна: ?) равна полусумме соединяемых ею сторон ?) одной из его сторон ?) равна половине параллельной стороны ?) равна полусумме медиан, проходящих через её концы Вопрос id:862931 Дан треугольник, стороны которого равны 6 см, 3 см, 5 см. Найдите периметр треугольника, вершинами которого являются середины сторон данного треугольника ?) 14 см ?) 7 см ?) 8 см ?) 28 см Вопрос id:862934 Длина тени дерева равна 10,2 м, а длина тени человека, рост которого 1,7 м, равна 2,5 м. Высота дерева равна ___ м Вопрос id:862935 Длина тени дерева равна 13,5 м, а длина тени человека, рост которого 1,8 м, равна 2 м. Высота дерева равна ___ м Вопрос id:862936 Для определения расстояния от точки А до недоступной точки В на местности выбрали точку С и измерили отрезок АС и углы ВАС и АСВ. Затем построили на бумаге треугольник A1B1C1, подобный треугольнику ABC. Найдите АВ, если АС = 42 м, А1С1 = 6,3 см, А1 В1 = 7,2 см ?) 52 м ?) 44 м ?) 46 м ?) 48 м Вопрос id:862937 Если в Δ АВС линия А1В1 || АВ, и при этом А1 – середина стороны АС, В1 – середина стороны ВС, то согласно теореме о средней линии треугольника линия А1В1 равна ?)  АВ АВ?) 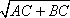 ?) 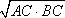 ?)  (ВС + АС) (ВС + АС)Вопрос id:862939 Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении ___, считая от вершины ?) 3 : 2 ?) 3 : 1 ?) 2 : 3 ?) 2 : 1 Вопрос id:862940 Метод ___ при решении задач на построение треугольника состоит в том, что сначала на основании некоторых данных строят треугольник, подобный искомому, а затем, используя остальные данные, строят искомый треугольник ?) уменьшения ?) подобия ?) масштабирования ?) увеличения Вопрос id:862941 Отрезок XY называется средним пропорциональным (или средним геометрическим) между отрезками АВ и CD, если ___ ?) XY = 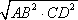 ?) XY = 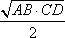 ?) 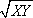 = АВ · СD = АВ · СD ?) XY = 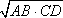 Вопрос id:862948 Отрезок, соединяющий середины двух сторон треугольника, называется ___ линией треугольника Вопрос id:862949 Периметр треугольника равен 12 см, середины сторон соединены отрезками. Периметр полученного треугольника равен ___ (число) см Вопрос id:862950 Периметр треугольника равен 6 м, середины сторон соединены отрезками. Периметр полученного треугольника равен ___ (число) м Вопрос id:862951 Примерами подобных фигур произвольной формы являются ?) две географические карты одного и того же района, выполненные в разных масштабах ?) две фотографии одного и того же предмета, сделанные при разных увеличениях ?) два прямоугольника, у которых две смежные стороны одного пропорциональны двум смежным сторонам другого ?) два квадрата Вопрос id:862952 Средняя линия треугольника ___ одной из его сторон Вопрос id:862953 Точки Р и Q – середины сторон АВ и АС треугольника ABC. Найдите периметр треугольника ABC, если периметр треугольника APQ равен 12 см ?) 18 см ?) 3 см ?) 6 см ?) 24 см Вопрос id:862954 Фигуры F и F1 называются ___, если каждой точке М фигуры F сопоставляется точка М1 фигуры F1 так, что точки М и М1 лежат на луче с началом в некоторой фиксированной точке О, причем OM1 = k · OM ?) центрально-симметричными ?) лучево-подобными ?) симметрично-подобными ?) центрально-подобными Вопрос id:862955 Фигуры F и F1 называются ___, если каждой точке фигуры F можно сопоставить точку фигуры F1 так, что для любых двух точек М и N фигуры F и сопоставленных им точек М1 и N1 фигуры F1 выполняется условие 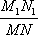 = k = kВопрос id:862957 На рисунке АВ и АС – отрезки касательных. Треугольники АВО и АСО:
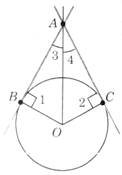
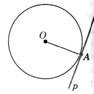
?) прямоугольные ?) остроугольные ?) тупоугольные ?) равны между собой Вопрос id:862958 На рисунке прямая р
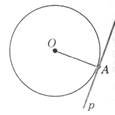
?) является касательной к окружности с центром О ?) является секущей к окружности с центром О ?) является хордой окружности с центром О ?) пересекает окружность с центром О Вопрос id:862960 На рисунке точка А является точкой ___ прямой и окружности
Вопрос id:862961 В треугольнике ABC угол В прямой. Верны ли утверждения? А) Прямая ВС является касательной к окружности с центром А радиуса АВ В) Прямая АС не является касательной к окружности с центром В и радиусами ВА и ВС Подберите правильный ответ ?) А - нет, В - нет ?) А - да, В -нет ?) А - да, В - да ?) А - нет, В - да Вопрос id:862962 Верны ли определения? А) Две касательные к окружности, проведенные в точках, принадлежащих одному и тому же диаметру, параллельны В) Диаметр окружности всегда больше любой ее хорды, не проходящей через центр этой окружности Подберите правильный ответ ?) А - нет, В - да ?) А - да, В - да ?) А - нет, В - нет ?) А - да, В - нет Вопрос id:862963 Верны ли определения? А) Через одну точку окружности можно провести только одну секущую В) Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания Подберите правильный ответ ?) А - да, В - нет ?) А - нет, В - нет ?) А - нет, В - да ?) А - да, В - да Вопрос id:862964 Верны ли определения? А) Диаметр окружности является ее хордой В) Диаметр окружности, проходящий через середину хорды, перпендикулярен ей Подберите правильный ответ ?) А - нет, В – да ?) А - нет, В – нет ?) А - да, В – да ?) А - да, В – нет Вопрос id:862965 Верны ли определения? А) Если две окружности имеют только одну общую точку, то они касаются в этой точке В) Через одну точку может проходить больше двух касательных к окружности Подберите правильный ответ ?) А - да, В - нет ?) А - нет, В - нет ?) А - да, В - да ?) А - нет, В - да Вопрос id:862966 Верны ли определения? А) Если расстояние от точки А до центра окружности меньше радиуса окружности, то любая прямая, проходящая через точку А, является секущей по отношению к данной окружности В) Если радиус ОМ окружности с центром О делит хорду АВ пополам, то касательная, проведенная через точку М, параллельна хорде АВ Подберите правильный ответ ?) А - нет, В - нет ?) А - да, В - да ?) А - да, В - нет ?) А - нет, В - да Вопрос id:862967 Верны ли определения? А) Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности В) Диаметр окружности, проходящий через середину хорды, перпендикулярен ей Подберите правильный ответ ?) А - да, В - да ?) А - нет, В - нет ?) А - да, В - нет ?) А - нет, В - да |
 1 =
1 =  27
27