Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийГеометрия (10 кл. БП)1Вопрос id:861110 Площадь боковой поверхности правильной треугольной пирамиды, описанной около конуса с радиусом основания 2 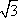 м и высотой 2 м, равна м и высотой 2 м, равна?) 36 м2 ?) 72 м2 ?) 24 м2 ?) 144 м2 Вопрос id:861111 Площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус которого равен 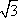 см, а высота 5 см, равна см, а высота 5 см, равна?) 10 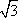 см2 см2?) 45 cм2 ?) 2,5 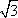 см2 см2?) 15p см2 Вопрос id:861112 Площадь боковой поверхности усеченного конуса, радиусы оснований которого 7 и 10 см, а высота 4 см, равна ?) 50p см2 ?) 68p см2 ?) 35p см2 ?) 85p см2 Вопрос id:861113 Площадь боковой поверхности цилиндра Sбок, радиус основания которого r, а высота h, может быть вычислена по формуле Sбок= ?) 2pr ?) 2prh ?) 2rh ?) prh Вопрос id:861114 Площадь боковой поверхности цилиндра радиуса 3 см и высоты 4 см равна ?) 24p см2 ?) 24 см2 ?) 12 см2 ?) 12p см2 Вопрос id:861115 Площадь боковой поверхности цилиндра радиуса ___ и высоты 4 см равна 24p см2 ?) 8 см ?) 3p см ?) 3 см ?) 8p см Вопрос id:861116 Площадь боковой поверхности цилиндра, периметр осевого сечения которого 10 м, а высота 3 м, равна ?) 3p м2 ?) 6 м2 ?) 6p м2 ?) 6p м Вопрос id:861117 Площадь боковой поверхности цилиндра, радиус которого 2 см, а высота 5 см, равна ___ см2 ?) 20p ?) 20 ?) 10 ?) 10p Вопрос id:861118 Площадь круга О1(О1А1), изображенного на рис. 17, равна ___, где ОА = 5 см, ОР = 10 см и О1Р = 2 см 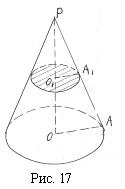 ?) 5 см2 ?) 1 см2 ?) p см2 ?) 5p см2 Вопрос id:861119 Площадь осевого сечения конуса, в который вписана правильная четырехугольная пирамиды с высотой 5 см и ребром основания 4 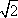 см, равна см, равна?) 40 см2 ?) 20 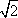 см2 см2?) 40 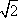 см2 см2?) 20 см2 Вопрос id:861120 Площадь основания и площадь осевого сечения цилиндра, диагональ развертки боковой поверхности которого, равная 9 см, образует с высотой развертки угол в 60°, соответственно равны ___ и ___ ?) 12,96 см2, 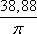 см2 см2?) 7,2 см2, 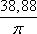 см2 см2?) 7,2 cм2, 38,88 cм2 ?) 12,96 см2, 38,88 см2 Вопрос id:861121 Площадь основания конуса, изображенного на рис. 17, равна ___, где О1А1 = 6 см и ОР:О1Р = 3:2 ?) 81p см2 ?) 324p см2 ?) 81 см2 ?) 16p см2 Вопрос id:861122 Площадь основания конуса, около которой описана правильная треугольная пирамида с боковым ребром 2 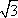 м и плоским углом при вершине 60°, равна м и плоским углом при вершине 60°, равна?) 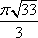 м2 м2?) p м2 ?) 1 м2 ?) 9p м2 Вопрос id:861123 Площадь полной поверхности конуса получается, если к площади его боковой поверхности прибавить ?) длину окружности основания ?) его радиус ?) площадь основания ?) его образующую Вопрос id:861124 Площадь полной поверхности конуса радиуса R, образующая которого l, может быть вычислена по формуле: 1) S = 2pR2 = pRl; 2) S = pR2 + pRl; 3) S = 2pR(R +l); 3) S = pRl ?) 4 ?) 3 ?) 1 ?) 2 Вопрос id:861125 Площадь полной поверхности конуса радиуса основания 8 см и высоты ___ равна 144p см2 ?) 6p см ?) 10 см ?) 10p см ?) 6 см Вопрос id:861126 Площадь полной поверхности правильной четырехугольной призмы, описанной около цилиндра радиуса 2 см и высоты 5 см, равна ?) 36 см2 ?) 52 см2 ?) 96 см2 ?) 112 см2 Вопрос id:861127 Площадь полной поверхности цилиндра Sцил радиуса r и высоты h может быть вычислена по формуле: 1) Sцил = 2pr + h; 2) Sцил = 2prh + r; 3) Sцил = prh +pr2; 4) Sцил = 2pr2+2prh ?) 3 ?) 2 ?) 1 ?) 4 Вопрос id:861128 Площадь полной поверхности цилиндра равна произведению ___ на сумму его радиуса и высоты ?) радиуса основания ?) площади основания ?) его высоты ?) длины окружности основания Вопрос id:861129 Площадь полной поверхности цилиндра радиуса ___ и высоты 3 см равна 80p см2 ?) 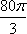 дм дм?) 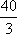 дм дм?) 8 дм ?) 5 дм Вопрос id:861130 Площадь полной поверхности цилиндра, изображенного на рис. 40, равна 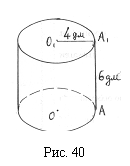 ?) 50p дм2 ?) 80p дм2 ?) (10p + 8) дм2 ?) (50p + 3) дм2 Вопрос id:861131 Площадь полной поверхности цилиндра, полученного из двух цилиндров радиуса 5 см и высоты 10 и 12 см соответственно, поставленных один на другой так, что их основания совпадают, равна ?) 150p см2 ?) 270 см2 ?) 270p см2 ?) 120p см2 Вопрос id:861132 Площадь поной поверхности конуса с радиусом основания 8 см и высотой 6 см неверно вычислена в случае… 1) 144p см2; 2) 144 см2; 3) (72p×2) см2; 4) (64p + 80p) см2 ?) 3 ?) 1 ?) 2 ?) 4 Вопрос id:861133 Площадь сечения плоскостью, перпендикулярной оси, в ___ раз(а) меньше площади основания, если радиус сечения в 2 раза меньше радиуса основания ?) 4 ?) 2 ?) 3 ?) 0,5 Вопрос id:861134 Площадь сечения шара радиуса 41 см плоскостью, отстоящей от его центра на 9 см, равна ?) 1600 см2 ?) 40p см2 ?) 40 см2 ?) 1600p см2 Вопрос id:861135 Поверхность называется цилиндрической, если она образована ___, заключенными между двумя параллельными плоскостями и перпендикулярными этим плоскостям. ?) параллельными кривыми ?) отрезками прямых ?) отрезками параллельных прямых ?) прямыми Вопрос id:861136 Поверхность, образованная всеми точками пространства, отстоящими от данной на данное расстояние, называется ?) цилиндром ?) сферой ?) шаром ?) конусом Вопрос id:861137 Под площадью полной поверхности цилиндра понимают ___ площадей оснований и боковой поверхности цилиндра ?) разность ?) сумму ?) произведение ?) частное Вопрос id:861138 Под площадью полной поверхности цилиндра понимают сумму площадей ___ и ___ цилиндра ?) основания, осевого сечения ?) одного из оснований, боковой поверхности ?) одного из оснований, другого основания ?) оснований, боковой поверхности Вопрос id:861139 Под телом вращения понимают тело, полученное при вращении плоской фигуры вокруг ?) прямой, перпендикулярной плоскости этой фигуры ?) произвольной точки ?) точки, лежащей в этой плоскости ?) прямой, лежащей в той же плоскости Вопрос id:861140 Под уравнением сферы понимают такое соотношение х, у, z, которому удовлетворяют координаты ?) которому не удовлетворяют координаты любой точки, не принадлежащей сфере ?) точек сферы ?) любой точки, принадлежащей сфере ?) х, у и z любой точки, принадлежащей сфере, и не удовлетворяют координаты любой точки, ей не принадлежащей Вопрос id:861141 Построение точки пересечения B прямой l, параллельной оси цилиндра, с его верхним основанием, когда точка пересечения с нижним основанием - точка А, изображено на рис. 9 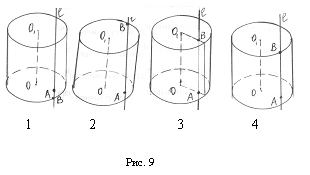 ?) 3 ?) 1 ?) 2 ?) 4 Вопрос id:861142 Правильную треугольную пирамиду высоты h см с ребром основания, равным а см, можно описать около конуса, имеющего ту же высоту и радиус основания, равный ?) а см ?) 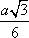 см см?) 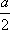 см см?) 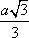 см смВопрос id:861143 Правильную треугольную пирамиду с ребром основания, равным 2 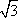 см, можно вписать в конус, имеющий ту же высоту и радиус основания, равный см, можно вписать в конус, имеющий ту же высоту и радиус основания, равный?) 1 см ?) 2 см ?) 1,5 см ?) 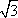 см смВопрос id:861144 Представление о цилиндрической поверхности дает поверхность ?) книги ?) воды в озере ?) яблока ?) ошкуренного бревна Вопрос id:861145 Представление о шаре дает ?) карандаш ?) резиновый мяч ?) мыльный пузырь ?) деревянный шар Вопрос id:861146 При вращении криволинейных трапеций, изображенных на рис. 52, 1 - 4, вокруг оси х получают соответственно 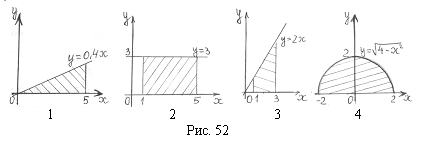 ?) конус, цилиндр, усеченный конус, полушар ?) конус, параллелепипед, усеченный конус ?) конус, цилиндр, усеченный конуса, шар ?) два треугольника, прямоугольник, трапеция, круг Вопрос id:861147 При записи уравнения сферы с центром в точке (1; 2; -3) радиуса 3 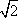 учащийся получил учащийся получил 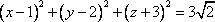 , допустив ошибку, которая состоит в том, что он , допустив ошибку, которая состоит в том, что он?) неверно записал вторую скобку ?) неверно записал третью скобку ?) не возвел в квадрат радиус ?) неверно записал первую скобку Вопрос id:861148 При известных площадях оснований S1 и S2 усеченного конуса удобно пользоваться формулой ___ для вычисления его объема V, а при известных радиусах r и R оснований ___ формулой ?) 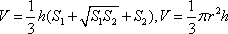 ?) 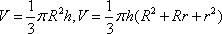 ?) 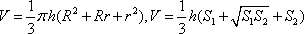 ?) 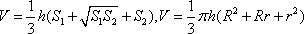 Вопрос id:861149 При подстановке значения радиуса R в выражение 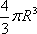 получаем ___ шара радиуса R получаем ___ шара радиуса R?) площадь поверхности ?) объем ?) число, на  превосходящее объем превосходящее объем?) объем  частей частейВопрос id:861150 Призма называется вписанной в цилиндр, если каждое ее основание ?) описано около соответствующего основания цилиндра ?) принадлежит соответствующему основанию цилиндра ?) вписано в соответствующее основание цилиндра ?) правильный треугольник Вопрос id:861151 Примером четырехугольной пирамиды, которую нельзя вписать в конус, служит пирамида, в основании которой лежит ?) параллелограмм, не являющийся прямоугольником ?) трапеция, боковые стороны которой равны ?) прямоугольник ?) квадрат Вопрос id:861152 Проекцией цилиндра может быть фигура, изображенная на рис. 6 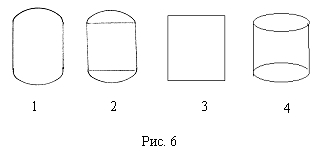 ?) 1 ?) 3 ?) 2 ?) 4 Вопрос id:861153 Произведение одной трети высоты на площадь основания конуса равно ___ этого конуса ?) площади основания ?) площади боковой поверхности ?) объему ?) площади полной поверхности Вопрос id:861154 Прямая 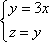 служит осью симметрии сферы служит осью симметрии сферы?) 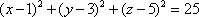 ?) 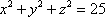 ?) 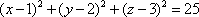 ?) 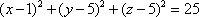 Вопрос id:861155 Прямая ___ служит осью симметрии сферы 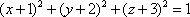 ?) 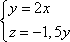 ?) 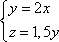 ?) 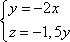 ?) 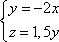 Вопрос id:861156 Прямая РО конуса, изображенного на рис. 13, является ?) осью ?) образующей ?) диаметром ?) высотой Вопрос id:861157 Прямая, содержащая высоту правильной треугольной пирамиды, вписанной в сферу, служит ___ этой сферы ?) одновременно центром и осью симметрии ?) плоскостью симметрии ?) центром симметрии ?) осью симметрии Вопрос id:861158 Прямая, содержащая центры оснований цилиндра, называется ?) радиусом цилиндра ?) осью цилиндра ?) образующей цилиндра ?) высотой цилиндра Вопрос id:861159 Прямой круговой цилиндр (или просто - цилиндр) - это ?) тело ?) поверхность ?) цилиндрическая поверхность ?) плоская фигура |
Copyright tests.ithead.ru 2013-2026