Тесты онлайн, бесплатный конструктор тестов. Психологические тестирования, тесты на проверку знаний.
Список вопросов базы знанийГеометрия (10 кл. БП)1Вопрос id:861210 Точка пересечения диагоналей куба, вписанного в сферу, служит ___ симметрии этой сферы ?) центром ?) одновременно центром и осью ?) плоскостью ?) осью Вопрос id:861211 Точка С - точка пересечения прямой АВ, где В - точка верхнего основания цилиндра, А - точка оси, с плоскостью нижнего основания цилиндра построена на рис. 7 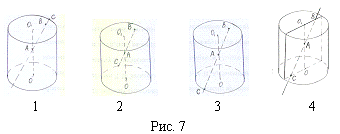 ?) 3 ?) 1 ?) 4 ?) 2 Вопрос id:861212 Угол наклона боковой грани правильной треугольной пирамиды с боковым ребром 2 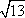 см, описанной около конуса с радиусом основания 2 см, описанной около конуса с радиусом основания 2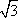 см, равен см, равен?) 30° ?) 90° ?) 45° ?) 60° Вопрос id:861213 Угол наклона боковой грани правильной четырехугольной пирамиды, боковое ребро которой 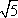 см, описанной около конуса радиуса 1 см, равен см, описанной около конуса радиуса 1 см, равен?) 45° ?) 60° ?) 90° ?) 30° Вопрос id:861214 Уравнение 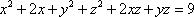 ___ уравнением сферы ___ уравнением сферы?) может быть ?) не является ?) всегда служит ?) является Вопрос id:861215 Уравнение 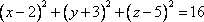 служит уравнением сферы с центром в точке ___, радиус которой равен служит уравнением сферы с центром в точке ___, радиус которой равен?) (2; -3; 5), 4 ?) (2; -3; 5), 16 ?) (2; 3; 5), 4 ?) (-2; 3; -5), 4 Вопрос id:861216 Уравнение прямой, параллельной оси Ох и ограничивающей сверху заштрихованный прямоугольник (рис. 58) в результате которого вокруг оси Ох получается тело, объем которого равен 144p куб. ед., имеет вид 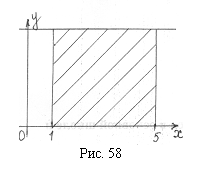 ?) у = 9 ?) х = 4 ?) х = 3 ?) у = 6 Вопрос id:861217 Уравнение сферы с центром в точке 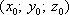 радиуса R имеет вид радиуса R имеет вид?) 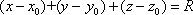 ?) 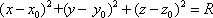 ?) 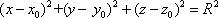 ?) 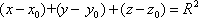 Вопрос id:861218 Уравнение сферы центром в точке ___ радиуса ___ имеет вид 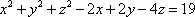 ?) (-1; 1; -2), 5 ?) (2; -2; 4), 5 ?) (1; -1; 2), 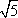 ?) (1; -1; 2), 5 Вопрос id:861219 Уравнение сферы, изображенной на рис. 29, имеет вид 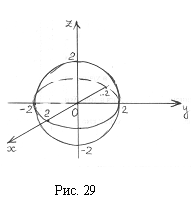 ?) 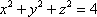 ?) 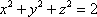 ?) 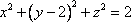 ?) 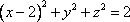 Вопрос id:861220 Усеченный конус - это ?) плоская фигура ?) тело ?) часть плоскости ?) поверхность Вопрос id:861221 Усеченный конус высоты 12 см, объем которого равен 244p см3, может иметь радиусы оснований ___ см и ___ см ?) 4,5 ?) 2, 10 ?) 3, 6 ?) 1, 3 Вопрос id:861222 Усеченный конус может быть получен при вращении фигуры ___, изображенной на рис. 19, вокруг прямой l 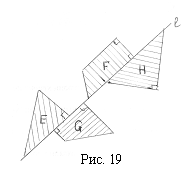 ?) F ?) G ?) E ?) H Вопрос id:861223 Утверждение “Любое сечение конуса плоскостью, перпендикулярной его оси, является кругом” ?) не всегда истинно ?) не всегда ложно ?) ложно ?) истинно Вопрос id:861224 Утверждение “Около любой сферы можно описать каждый из пяти правильных многогранников” ?) не всегда истинно ?) истинно ?) ложно ?) иногда ложно Вопрос id:861225 Утверждение “Около цилиндра, можно описать прямоугольный параллелепипед, ни одна грань которого не является квадратом” ?) иногда истинно ?) истинно ?) иногда ложно ?) ложно Вопрос id:861226 Утверждение “Осевым сечением цилиндра является квадрат тогда и только тогда, когда высота цилиндра равна диаметру его основания” ?) истинно ?) не всегда истинно ?) ложно ?) не всегда ложно Вопрос id:861227 Утверждение “Основанием конуса является окружность” ?) иногда ложно ?) иногда истинно ?) истинно ?) ложно Вопрос id:861228 Утверждение “Осью симметрии фигуры, состоящей из сферы и правильной треугольной пирамиды, описанной около этой сферы, служит прямая, содержащая высоту пирамиды” ?) ложно ?) иногда истинно ?) не всегда ложно ?) истинно Вопрос id:861229 Утверждение “Прямая 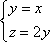 служит осью симметрии сферы служит осью симметрии сферы 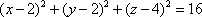 ” ”?) не всегда истинно ?) ложно ?) не всегда ложно ?) истинно Вопрос id:861230 Утверждение “Сфера симметрична относительно середины высоты правильной треугольной пирамиды, описанной около этой сферы” ?) иногда истинно ?) истинно ?) ложно ?) иногда ложно Вопрос id:861231 Утверждение “Сфера симметрична относительно точки пересечения диагоналей вписанного в нее куба” ?) истинно ?) ложно ?) иногда истинно ?) иногда ложно Вопрос id:861232 Утверждение “Сфера симметрична относительно центра основания описанного около нее куба” ?) иногда истинно ?) истинно ?) не всегда ложно ?) ложно Вопрос id:861233 Утверждение: “В конус всегда можно вписать треугольную пирамиду” ?) ложно ?) не всегда истинно ?) не всегда ложно ?) истинно Вопрос id:861234 Утверждение: “В любой конус можно вписать любую треугольную пирамиду” ?) не всегда ложно ?) истинно ?) не всегда истинно ?) ложно Вопрос id:861235 Утверждение: “Для того, чтобы объединение конуса и шарового сегмента представляло собой шаровой конус, необходимо и достаточно, чтобы они имели общее основание и были расположены по разные стороны от него” ?) истинно ?) не всегда ложно ?) иногда истинно ?) ложно Вопрос id:861236 Утверждение: “Любая сфера и любая плоскость пересекаются по окружности” ?) истинно ?) ложно ?) иногда истинно ?) не всегда ложно Вопрос id:861237 Утверждение: “Любую треугольную пирамиду можно описать около соответствующего конуса” ?) истинно ?) не всегда ложно ?) ложно ?) не всегда истинно Вопрос id:861238 Утверждение: “Любую четырехугольную пирамиду можно вписать в соответствующий конус” ?) иногда ложно ?) не всегда истинно ?) ложно ?) истинно Вопрос id:861239 Формула 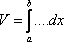 позволяет вычислить объем V тела, полученного при вращении криволинейной трапеции, изображенной на рис. 51 позволяет вычислить объем V тела, полученного при вращении криволинейной трапеции, изображенной на рис. 51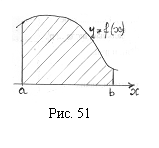 ?) 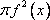 ?) 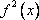 ?) 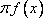 ?) 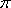 Вопрос id:861240 Центр симметрии сферы, описанной около правильной треугольной пирамиды, лежит на ___ этой пирамиды ?) ребре основания ?) основании ?) боковом ребре ?) высоте Вопрос id:861241 Центр сферы удален от плоскости ромба, диагонали которого равны 15 см и 20 см и все стороны которого касаются сферы радиуса 10 см, на расстояние, равное ?) 64 см ?) 2 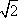 см см?) 36 см ?) 8 см Вопрос id:861242 Цилиндр высоты 4 и радиуса основания 3 получается в результате вращения вокруг оси х фигуры, изображенной на рис. 54 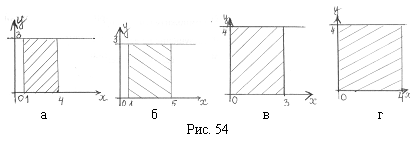 ?) а ?) в ?) б ?) г Вопрос id:861243 Цилиндр ограничен цилиндрической поверхностью и ?) двумя кругами ?) двумя окружностями ?) плоскостью ?) одним кругом Вопрос id:861244 Цилиндр, полученный при вращении фигуры, изображенной на рис. 53, вокруг оси х, имеет высоту ___ и радиус основания 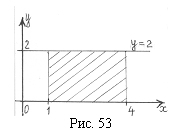 ?) 2, 3 ?) 3, 2 ?) 4, 4 ?) 3, 4 Вопрос id:861245 Цилиндрическая поверхность изображена на рис. 1 (а, б, в, г) 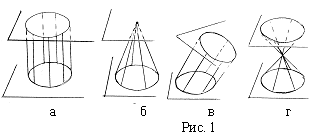 ?) г ?) б ?) а ?) в Вопрос id:861246 Цилиндрическая поверхность, ограничивающая цилиндр, называется ___ цилиндра ?) образующей ?) боковой поверхностью ?) основанием Вопрос id:861247 Цилиндрической называется ___, образованная отрезками параллельных прямых, заключенными между двумя параллельными плоскостями и перпендикулярных этим плоскостям ?) поверхность ?) сфера ?) плоскость ?) окружность Вопрос id:861248 Цилиндрической называется поверхность, образованная отрезками параллельных прямых, ___ перпендикулярных этим плоскостям ?) концами на двух плоскостях ?) заключенными между двумя плоскостями ?) лежащими между двумя плоскостями ?) заключенными между двумя параллельными плоскостями Вопрос id:861249 Часть шара, заключенную между двумя параллельными секущими плоскостями, называют ?) шаровым слоем ?) осевым сечением ?) шаровым сегментом ?) частью сферы Вопрос id:861250 Чтобы объем шара был 1 м3, необходимо, чтобы его радиус равнялся ___ м ?) 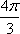 ?) 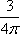 ?) 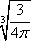 ?) 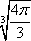 Вопрос id:861251 Шар - это тело, которое получается в результате вращения фигуры ___, изображенной на рис. 31, вокруг прямой а 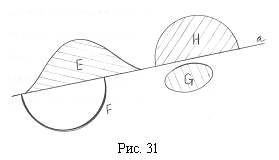 ?) F ?) G ?) E ?) Н Вопрос id:861252 Шар может быть получен вращением фигуры 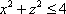 вокруг вокруг?) оси Ох ?) прямой z = -3 ?) прямой у = 2 ?) оси Оу Вопрос id:861253 Шар может быть получен вращением фигуры, заданной условием ___, вокруг оси Ох ?) 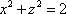 ?) 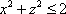 ?) 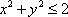 ?) 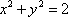 Вопрос id:861254 Шар получается при вращении фигуры F (рис. 42) вокруг прямой 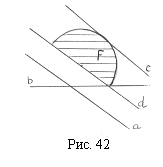 ?) d ?) a ?) c ?) b Вопрос id:861255 Шар с центром в начале координат радиуса 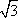 задается условием задается условием?) 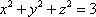 ≤ 3 ≤ 3?) 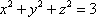 ?) 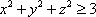 ?) 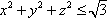 Вопрос id:861256 Шар с центром в точке А(1; -2; 5) радиуса 6 задается условием ?) 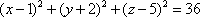 ?) 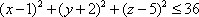 ?) 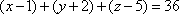 ?) 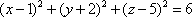 Вопрос id:861257 Шар, заданный условием 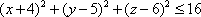 , имеет центр Р(..;..;..) и радиус R = … , имеет центр Р(..;..;..) и радиус R = …?) Р(4; 5; 6), 4 ?) Р(4; -5; 6), 4 ?) Р(-4; 5; 6), 16 ?) Р(-4; 5; 6), 4 Вопрос id:861258 Шаровой пояс высоты 2 см, радиусы основания которого 1 см и 5 см, получен сечениями шара радиуса ___ см ?) 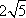 ?) 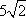 ?) 5 ?) 2 Вопрос id:861259 Шаровой сегмент не получится при вращении фигуры ___ (рис. 44) вокруг прямой 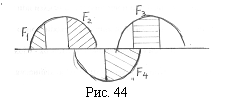 ?) F2 ?) F3 ?) F4 ?) F1 |
Copyright tests.ithead.ru 2013-2026